はいさい。ツシマです。
前回は平均を比較するt検定を解説しましたが、次はマンホイットニーU検定について説明していきます。
そもそも、マンホイットニーU検定って何?
簡単に言うと…
「2つのグループの違いを、平均じゃあなくて順位で比べよう!!」という検定です。
t検定が「平均血圧の差」を見るのに対し、
U検定は「血圧の高い人が、どっちのグループに多い?」みたいに順位で勝負。
健康対決!A部署 VS B部署
あなたは産業保健師です。健康診断の結果を分析しています。
では、今回の分析の登場人物に登場していただきましょう。パチパチパチパチ。
- A部署:健康意識高い系。通勤時間にウォーキングをすることが流行っている。昼は進んでサラダを食べる。
- B部署:仕事終わりにラーメンとビール。運動??そんなの都市伝説じゃあないですか?ファンタジーやメルヘンじゃあないんですから。
しかし!!!
B部署には「謎の筋トレオタク・小林君」が混じっていて、血圧も体脂肪率も健康的!!
まずは、前回の主人公、t検定に登場してもらいましょう。
t検定「A部署とB部署の平均体脂肪率を見るで。」
しかし、B部署には「謎の筋トレオタク・小林君」がいるので、平均が歪んで正しい結果を望めなくなります。
つまり、t検定は外れ値に弱いのです…
マンホイットニーU検定参戦!!
こんな状況の時、今回の主人公・マンホイットニーU検定の出番です。
保健師「健康診断結果、どう見てもA部署の方が良さそうなのに、B部署に筋トレオタク・小林君がいるからB部署の体脂肪率の平均が下がらない…!」
マンホイットニーU検定「全体ん順位ば見て、”健康な人”がどっちに多かかばちゃんと見るばい」
U値とは?
それぞれの順位をもとに計算する「勝ち数」です。
A部署 vs B部署、どれだけ上位を多く取ったか?
簡単に言えば、「健康ポイント、どっちが多いかバトル」です。
実践!マンホイットニーU検定
では、今回も架空のデータを使って実践をしていきます。
| 部署 | 氏名 | 体脂肪率(%) |
| A部署 | A01 | 20.7 |
| A部署 | A02 | 19.8 |
| A部署 | A03 | 21 |
| A部署 | A04 | 22.3 |
| A部署 | A05 | 19.6 |
| A部署 | A06 | 19.6 |
| A部署 | A07 | 22.4 |
| A部署 | A08 | 21.2 |
| A部署 | A09 | 19.3 |
| A部署 | A10 | 20.8 |
| A部署 | A11 | 19.3 |
| A部署 | A12 | 19.3 |
| A部署 | A13 | 20.4 |
| A部署 | A14 | 17.1 |
| A部署 | A15 | 17.4 |
| B部署 | B01 | 26.6 |
| B部署 | B02 | 25.5 |
| B部署 | B03 | 28.8 |
| B部署 | B04 | 25.7 |
| B部署 | B05 | 24.5 |
| B部署 | B06 | 31.7 |
| B部署 | B07 | 27.4 |
| B部署 | B08 | 28.2 |
| B部署 | B09 | 24.4 |
| B部署 | B10 | 26.6 |
| B部署 | B11 | 28.3 |
| B部署 | B12 | 25.1 |
| B部署 | B13 | 28.9 |
| B部署 | B14 | 26.5 |
| B部署 | B15 | 27.3 |
| B部署 | B16 | 26.5 |
| B部署 | B17 | 32.6 |
| B部署 | B18 | 28 |
| B部署 | B19 | 25.4 |
| B部署 | 筋トレオタク・小林君 | 12 |
※今回はデータをわかりやすく表記していますが、くれぐれも実際の従業員のデータに筋トレオタクとか書かないでください。あと匿名化はきっちりやりましょう。
早速ExcelでマンホイットニーU検定をやっていきますが、Excelではp値は近似値しか出すことができません。また、標本が小さすぎる(データが10個以下など)場合は不正確になります。
実務に活かすのに参考にするのであれば問題ないこともあると思いますが、論文レベルでは厳密な計算(例:Pytyonを使った計算)が必要です。
1. 体脂肪率に順位をつける
=RANK.EQ([@体脂肪率(%)], 体脂肪率全体の範囲, 1)
で体脂肪率が低い順に順位がつけられます。

2. A部署とB部署の順位の合計をそれぞれ計算する
=SUMIFS(順位列, 部署列, “A部署”)
同様にB部署も計算します。

3. 部署ごとの人数を合計する
部署ごとの人数(n)を用意します。ここでは便宜上、A部署の人数をnA、B部署の人数をnBとします。

4. U値を求める
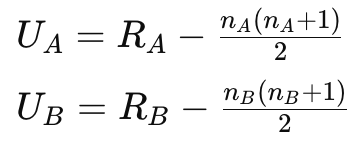
※R = 順位合計、n = 各部署の人数
部署ごとにU値を求めます。

UAとUBを比較し、小さい方がU値です。
今回の計算では、UA=11、UB=283ですので、U値は11です。
さて、このU値の判断方法ですが、値が極端に小さい(または大きい)と、差があると考えられます。
先ほど作った体脂肪率の順位を、一度1位から順番に並べてみます。
| 部署 | 氏名 | 体脂肪率(%) | 順位 |
| B部署 | 筋トレオタク・小林君 | 12 | 1 |
| A部署 | A14 | 17.1 | 2 |
| A部署 | A15 | 17.4 | 3 |
| A部署 | A09 | 19.3 | 4 |
| A部署 | A11 | 19.3 | 4 |
| A部署 | A12 | 19.3 | 4 |
| A部署 | A05 | 19.6 | 7 |
| A部署 | A06 | 19.6 | 7 |
| A部署 | A02 | 19.8 | 9 |
| A部署 | A13 | 20.4 | 10 |
| A部署 | A01 | 20.7 | 11 |
| A部署 | A10 | 20.8 | 12 |
| A部署 | A03 | 21 | 13 |
| A部署 | A08 | 21.2 | 14 |
| A部署 | A04 | 22.3 | 15 |
| A部署 | A07 | 22.4 | 16 |
| B部署 | B09 | 24.4 | 17 |
| B部署 | B05 | 24.5 | 18 |
| B部署 | B12 | 25.1 | 19 |
| B部署 | B19 | 25.4 | 20 |
| B部署 | B02 | 25.5 | 21 |
| B部署 | B04 | 25.7 | 22 |
| B部署 | B14 | 26.5 | 23 |
| B部署 | B16 | 26.5 | 23 |
| B部署 | B01 | 26.6 | 25 |
| B部署 | B10 | 26.6 | 25 |
| B部署 | B15 | 27.3 | 27 |
| B部署 | B07 | 27.4 | 28 |
| B部署 | B18 | 28 | 29 |
| B部署 | B08 | 28.2 | 30 |
| B部署 | B11 | 28.3 | 31 |
| B部署 | B03 | 28.8 | 32 |
| B部署 | B13 | 28.9 | 33 |
| B部署 | B06 | 31.7 | 34 |
| B部署 | B17 | 32.6 | 35 |
明らかにA部署の上位ランカーが多いですね。
つまり、A部署の順位の「数字」を足していくと、小さい数になります。
逆にB部署の順位の「数字」は、大きな数になります。
5. Z値を計算する
Z値とは、あるデータが「平均」からどれだけ離れているかを、「標準偏差(σ)」の単位で表したものです。
簡単に言えば、データから標準化された位置です。
Z値の公式は以下のとおりです。

式の中にある謎の文字は以下のとおりです。

ここで、Excelで片側検定を行います。
片側検定についてはt検定の記事に載せたので参照してください。
「最終的に両側検定がしたいのに、なぜここで片側検定をするのか?」と思う方もいらっしゃると思いますが、後の手順で使用するExcelの関数(NORM.S.DIST)は左側の片側確率しか出すことができないからです。
では、Excelでどのように入力すれば良いのかと言うと、
= (U値 – (nA * nB / 2)) / SQRT(nA * nB * (nA + nB + 1) / 12)

6. p値を求める(両側検定)
両側検定のp値を求めると、
= 2 * NORM.S.DIST(-ABS(Z値), TRUE)

p値の表記がエラーに見えなくもないですが、
3.59824E-06 = 3.59824×10-6=0.00000359824
つまり、p値が有効水準0.05を大きく下回っていることを示します。(有意水準についての詳しい説明はt検定の記事を参照してください)
今回の結果は偶然出たものではなかったのです。
まとめ
以上、ゆるっとマンホイットニーU検定の解説をしてきました。
筋トレオタク・小林君のような外れ値を持つ人がいても、集団の特徴を見ることができるのがマンホイットニーU検定です。
まるでゲームのランクを2つの集団で競っているような検定でした。
t検定とは違った意味で面白い検定なので、皆さんもぜひ使ってみてください!
おまけ PythonでマンホイットニーU検定
では、次はPythonを使って、もっと正確にマンホイットニーU検定を行います。
import pandas as pd
from scipy.stats import mannwhitneyu
#データ読み込み
path = 'ファイルパス名'
df = pd.read_excel(path)
# グループ分け
a_group = df[df['部署'] == 'A部署']['体脂肪率(%)']
b_group = df[df['部署'] == 'B部署']['体脂肪率(%)']
# マンホイットニーU検定(両側)
stat, p_value = mannwhitneyu(a_group, b_group, alternative='two-sided')
print(f'U値: {stat}')
print(f'p値: {p_value}')
出力:
U値: 15.0
p値: 7.273200294168801e-06
