こんにちは、ツシマです。
t検定、マンホイットニーU検定、カイ二乗検定に引き続き、今回は相関係数を紹介していきます!
そもそも、相関係数って?

相関係数(correlation coefficient)とは、2つの変数がどれくらい“仲良し”かを数値で表すものです。
1.0なら「シンクロ率100%の大親友」です。
ちなみに-1.0なら「息を吸うように反対行動を取る、ライバル関係」です。0.0なら「赤の他人」です。
ルパン三世と次元大介が1.0、ルパン三世と銭形警部が-1.0、ルパン三世とピカチュウは接点がないので0みたいなもんです(でもルパン三世と銭形警部って意外と仲良いような…?)
では、医療の世界にも当てはめてみましょう。
【例1:体重と血圧】
「体重が増えると血圧も上がる」→これは相関係数が正の値(+)になりそうですね。正の相関(+)です。
これは看護師や保健師としては「太ったら血圧あがるの当たり前じゃん」っていうあの感覚です。
【例2:ストレスと睡眠の質】
「ストレスが上がると、睡眠の質が下がる」→これも相関がありますね。しかしこっちは負の相関(−)です。
どちらかが上がると、もう一方は下がる関係です。
気をつけろ、これは罠だ!
一見便利そうな相関係数ですが、落とし穴もあります。
「相関≠因果」
これだけは覚えてください!!!よくある勘違いです!!!
例えば、「アイスクリームの売り上げと熱中症の件数に強い相関がある」と言われても、「アイスクリームを食べたら熱中症になる」訳ではありません。
アイスクリームの売り上げも熱中症の件数も、どちらも「暑さ」が原因ですもんね。
そのため、保健師としては「相関がある」と言われても、「ほんと?」と一度立ち止まる冷静さが必要です。
他にも、相関係数を「信用してはいけない時」があります。
- 外れ値が大きい時

例として、クラス全員身長160~170cmなのに、なぜか1人だけ240cmの謎の巨人がいるという状況を考えてみましょう。
普通なら身長と体重にキレイな相関が出るはずなのに、その巨人がいるだけで、データがぐちゃぐちゃになり、相関係数も変な値になります。
たった1人の異次元が、全体の空気を壊すみたいなもんです。
現実でも、1人だけ無茶苦茶な人がいると集団の空気が壊れますよね?
- データの中に複数のグループが含まれている時
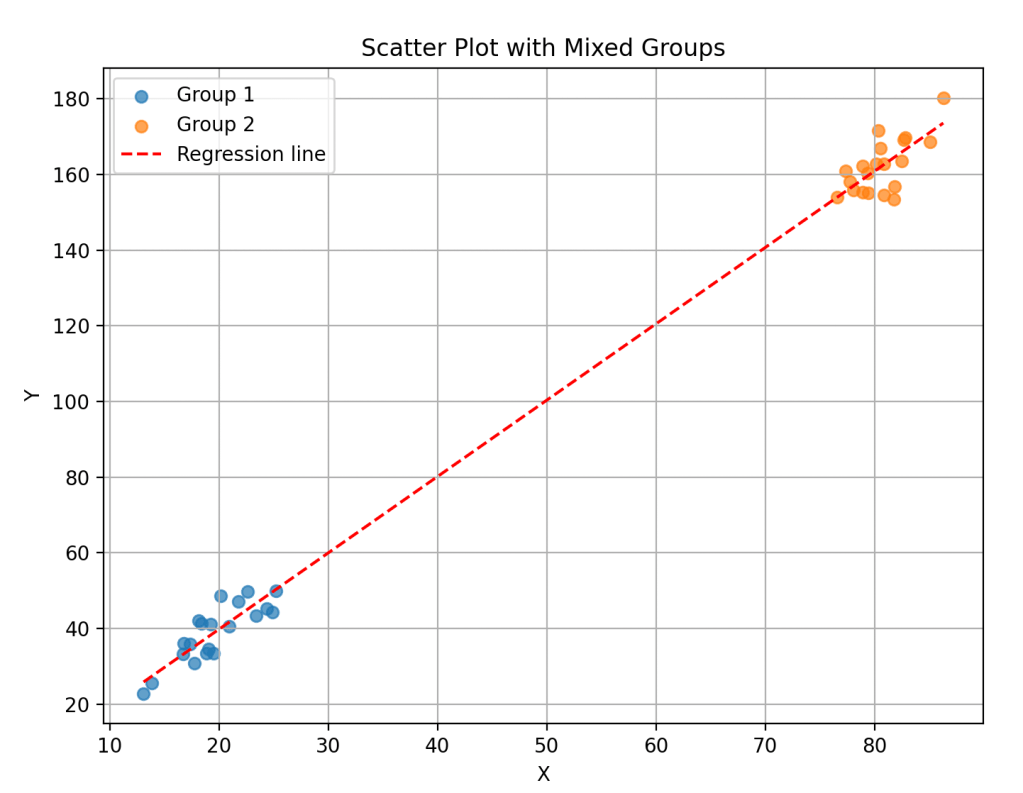
例として、アメフト部の学生集団(筋肉バキバキ、体重が重くても健康)と、茶道部の学生集団(筋肉バキバキはほとんどいない、体重が重いと健康リスクあり)を一緒にして分析してはいけないということです。
「体重と健康のリスクには相関ありません!」とおかしな結果が出る可能性があります。
「体育会系と文化系を一緒にすんな!!」ということです。グループの性質が違うのに、無理矢理まとめるのはやめましょう。
- 相関係数が0または0に近い時

相関係数が0だからといって、説明できる関係性がないとは限りません。
例えば、ストレスと睡眠時間が「低い→高い→また低い」とカーブする関係だったら、例え相関係数が0だったとしても関係がないとは言えませんよね。
色々ある、相関係数
実は相関係数は複数の種類があります。
ピアソンの積率相関係数
データ同士を「まっすぐ直線でつなげる関係」だけを見ています。
例えば「体重が増えたら、血圧も増える」みたいな関係です。
しかし、ピアソンは直線にうるさいので、データに少しでもカーブがあるとすぐに機嫌を損ねます。相関係数がおかしくなるのです。
また、先ほどの相関係数の罠で書いたように、外れ値にとても弱いのです。
ただし、直線関係についてはピアソンの右に出るものはいません。
順位相関係数
データの「順位」を気にして相関係数を見るのが順位相関係数です。
2種類あります。
スピアマンの順位相関係数
とにかく「順位」を気にする相関係数です。
データの中身の細かい数字は、正直どうでもいいタイプです。
とにかく、「1位は誰だ?」「2位は誰だ?」と順位の並び順が揃っているかを見ています。
大雑把で細かいデータの内容を無視してしまうため、量の大小を考えずに相関係数を出してしまいます。また、同じ順位(タイ)が多いと相関係数が歪みます。
しかし、例えデータの並びがぐにゃぐにゃに曲がっていても、「順位さえ合っていればOK!」というおおらかな相関係数です。
ケンドールの順位相関係数
スピアマンとは違ってガツガツせず、
データの順位のペアをそっと比較し、「この2人の順位はちゃんと揃っているかな?」と丁寧に見ていきます。
しかもケンドールは、小さいデータに強いです。
データ数が少ない時でも、きちんと優しく正確に関係を教えてくれます。
しかし、データのペアをいちいち全部並べるため、データ数が多いと計算量がとんでもなく多くなり、かなり重くなります。
だから、サンプル数が100人、200人、1000人…とか多くなると、ケンドールに頼るのは避けたほうが良いのです。
また、ピアソン、スピアマンとは違って標準のExcelでやると骨が折れるのです…残念。
計算ソフトを使って求めましょう。
Excelでやってみた、相関係数の計算
今回使うデータはこちら!
| X | Y |
| 58.8 | 48.5 |
| 57.6 | 60.6 |
| 66 | 60.4 |
| 77.9 | 63.5 |
| 81.6 | 69.7 |
| 72.9 | 61.6 |
| 88.1 | 85.4 |
| 88.1 | 68.5 |
| 93.9 | 78.3 |
| 102.1 | 73.1 |
ここからXとYの関係を見てみましょう!
散布図と回帰直線
まず、どんな分布になっているか、「散布図」と「相関を示す線(回帰直線)」を同時に表示します。
XとYの表を選択し、「挿入」→「散布図」を選択します。マーカー(点)のみがあるものを選んでください。


散布図はできましたが、なんだかタイトルが変なので、「Y」というタイトルをダブルクリックして「相関」にしてしまいましょう。

続いて、回帰直線を作ります。
散布図上のプロットされた点を右クリックし、メニューから「近似曲線の追加」を選択してください。


「近似曲線の書式設定」が開きます。
「近似曲線のオプション」を「線形近似」にし、「グラフに数式を表示する」、「グラフにR-2乗値を表示する」にチェックを入れます。

これで、数式とR-2乗値が表示されました。
R-2乗値(決定係数)はピアソンの相関係数を2乗したものです。おおよその相関の目安が表示されます。
続いて、ピアソンの積率相関係数とスピアマンの順位相関係数を求めていきます。ケンドールの順位相関係数は複雑すぎるので今回は省略します。
ピアソンの積率相関係数
これは一番簡単。
=CORREL(比較したいデータAがある範囲,比較したいデータBがある範囲)を入力するだけです!
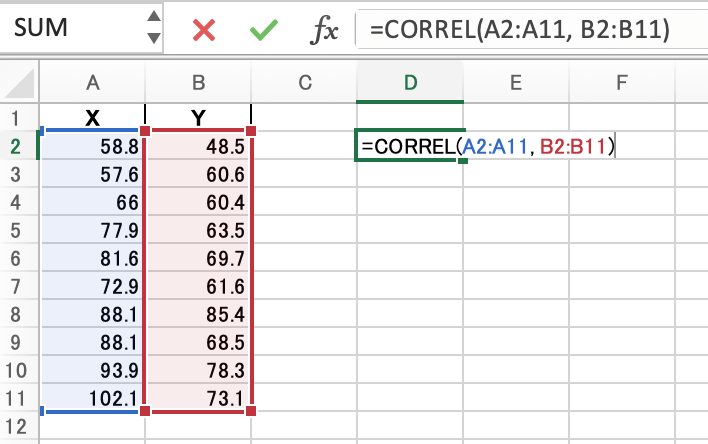
結果、ピアソンの積率相関係数は0.80693でした。
次に、p値を求めてみます。
公式は下記の通りです。
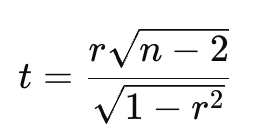
まず、r(相関係数)とn(データのペアの数)を使って、tを計算します。
今回はデータのペアが10個あるため、n=10です。
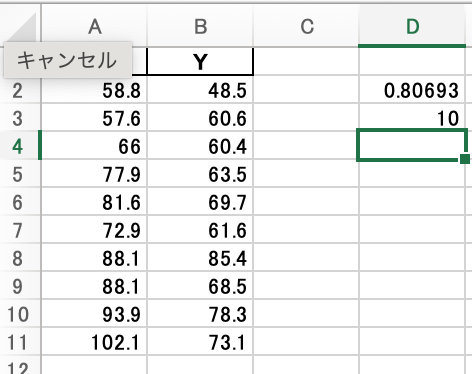
そして、= (相関係数セル * SQRT(データのペア数セル-2)) / SQRT(1 – 相関係数セル^2)でt値を求めます。

この結果がt値です。
次に、自由度n-2を使い、p値を求めます。
=T.DIST.2T(ABS(t),自由度)を使って求めます。
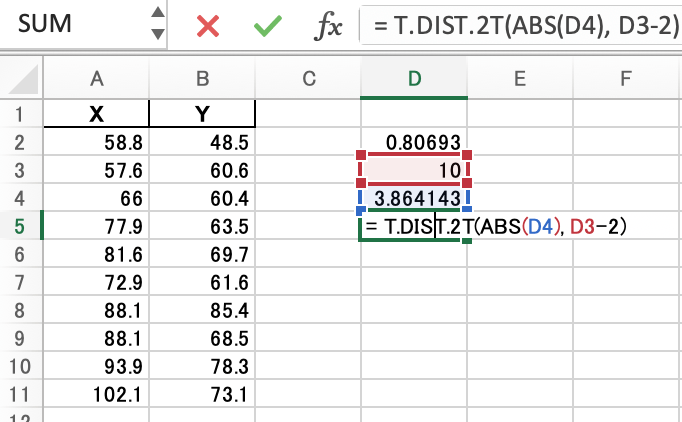

今回のp値は、0.004781でした。
有意水準0.05を考えると、この相関係数は統計学的に有意です。
スピアマンの順位相関係数
別の列に、XとYそれぞれRANK関数で順位をつけます。
(例えば、C列に「Xの順位」、D列に「Yの順位」)
=RANK(順位をつけたいデータがあるセル,順位をつけたいデータの範囲)
で求めます。
今回の場合、データが大きいものから順に1位になっています。

同じように他のデータも順位をつけていきます。
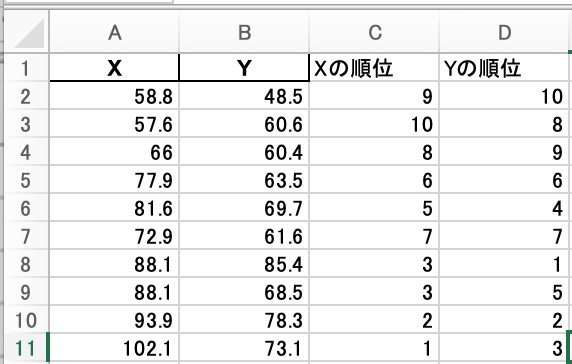
そして、ピアソンと同じくCORREL関数を使います。

スピアマンの順位相関係数は0.88833632でした。
p値はピアソンの場合と同じ方法では正確なものは求められません。
それは、ピアソン相関は「連続量データ」+「正規分布を仮定」で成り立っているからです。
スピアマンは「順位データ」なので、本来は別の理論(順位検定)に基づきます。
しかし実務上、データが十分に多い(データのペアが20個以上)なら、スピアマンの相関係数も大体t分布に従うとみなして良い、という取り扱いがされることもあります。
つまり、サンプルが少なすぎなければ、スピアマンでもピアソンのp値の求め方は近似的に使えます。
まとめ
以上、今回は相関係数についてまとめました。
皆さんも「罠」に引っ掛からず、冷静に相関係数を判断しましょう!
おまけ Pythonで分析
コード:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
from scipy.stats import kendalltau, spearmanr, pearsonr
# Excelデータ読み込み
df = pd.read_excel('ファイルパス名')
# データ取得
x = df['X']
y = df['Y']
# 3つの相関係数とp値を計算
pearson_corr, pearson_p = pearsonr(x, y)
spearman_corr, spearman_p = spearmanr(x, y)
kendall_corr, kendall_p = kendalltau(x, y)
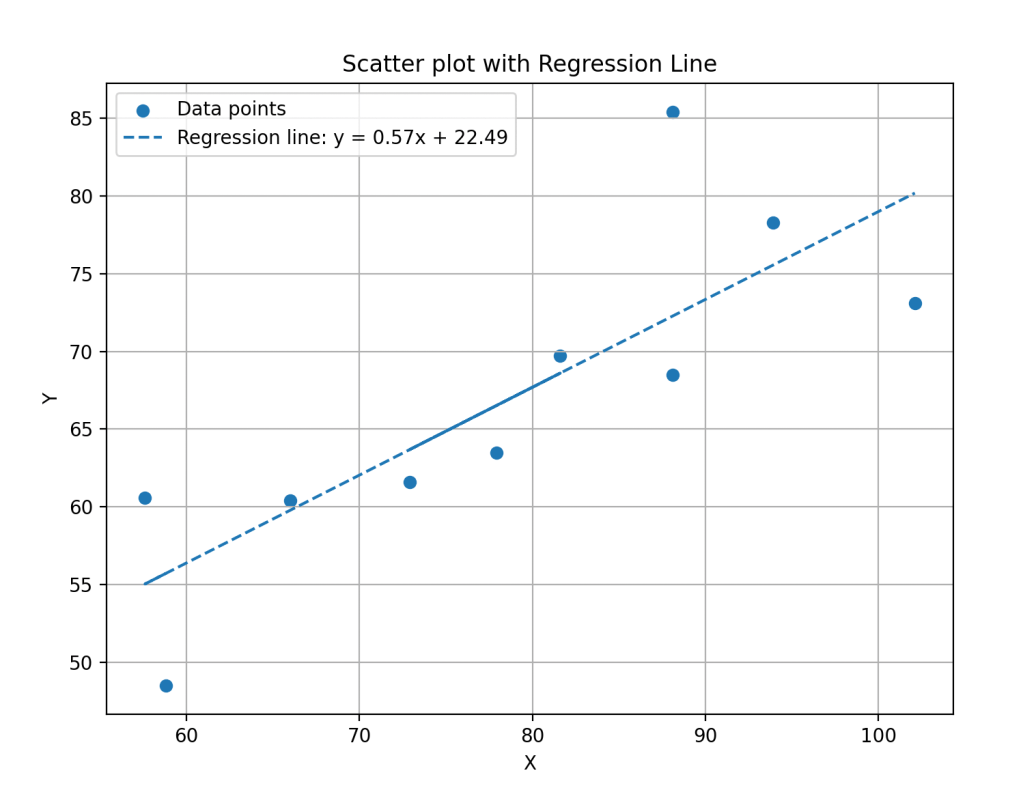
# 散布図+回帰直線の作成
slope, intercept, r_value, p_value, std_err = stats.linregress(x, y)
line = slope * x + intercept
plt.figure(figsize=(8, 6))
plt.scatter(x, y, label='Data points')
plt.plot(x, line, label=f'Regression line: y = {slope:.2f}x + {intercept:.2f}', linestyle='--')
plt.title('Scatter plot with Regression Line')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()
# 相関係数とp値の表示
print(f"ピアソン相関係数: {pearson_corr:.3f}, p値: {pearson_p:.3f}")
print(f"スピアマン相関係数: {spearman_corr:.3f}, p値: {spearman_p:.3f}")
print(f"ケンドール相関係数: {kendall_corr:.3f}, p値: {kendall_p:.3f}")
出力:
ピアソン相関係数: 0.807, p値: 0.005
スピアマン相関係数: 0.881, p値: 0.001
ケンドール相関係数: 0.719,p値: 0.004
ケンドール相関係数も簡単に表示できます。
そう、Pythonならね。
それにPythonは、p値については、
ピアソン:普通の連続データ用。標準(t検定)でOK。
スピアマン:順位データではあるが、Pythonはきちんと専用検定を使っている(近似も含めて正しい)
ケンドール:データ数が少なければ正確な方法、大きければ正規近似をしてきちんとp値を出している
つまり、統計学的な手法に合わせてp値を求めてくれます。ありがたい!!!