3つのデータの違いを調べたい。でも…
おはこんハロチャオ。
突然ですが、皆さんはこんな状況に出くわしたこと、ありませんか?
「部署A・B・C、それぞれのストレスレベルに差があるのか知りたい。でも、データは偏ってるし、正規分布なんてしてなさそう…」
はい、そんな時には、
Kruskal-Wallis検定の出番です!
Kruskal-Wallis検定ってなんぞや?
Kruskal-Wallis検定とは、
「3つ以上のグループの平均の順位に差があるかを調べるノンパラメトリック検定」です。
つまり、
- 「平均値」ではなく「平均の順位」で勝負!!
- 「正規分布」じゃなくてもOK!!
- 「等分散」ではない?でもそんなの関係ねぇ!!
という、データがやんちゃでわがまま放題でも優しく受け止めてくれる懐の深い検定です。
どんな時に使えるの?
例えばこんなとき…
- 部署A・B・Cで看護師の疲労度スコアを比べたい
- 4つの部署で生活習慣スコアの違いを見たい
- 3種類の勤務形態(常勤、非常勤、夜勤専従)でQOLを比較したい
でも、データの分布がバラバラだったり、異常値が多かったり、明らかに正規分布してない…
そんな時に「私の出番かしら?」と穏やかにやってくるのがKruskal-Wallis検定です。
どうやってやるの??
ざっくりな手順は、
- データを全てまとめて、順位をつける
- 各グループの順位の合計を計算
- 差が大きいほど、グループ間に「違い」があると判定
そして、最後に出てくるのが、みなさんお馴染みのp値です。
これが0.05未満だったら「少なくともどこかに差があります!」と教えてくれます。
しかーーーーし。
Kruskal-Wallis検定はANOVAと同様、どのグループに差があるかは教えてくれません。
そこで登場するのが 多重比較 や グラフによる可視化です。
特にグラフによる可視化はおすすめ。統計が苦手な人にとってもわかりやすいです。
注意事項は?
さて、ここではありがちなミスをご紹介します。
みんなでこの落とし穴を回避ちゃいましょう。
- これは「3グループ以上」で使う検定です。2グループならマンホイットニーU検定でOKです!
- 対応のあるデータには使えません(例:同じ人の前後比較など)。対応のあるデータにはFriedman検定を使いましょう!
- p値が有意でも、すぐに「Aが一番悪い!」などと断言しないでください。どことどこに差があったのかを調べましょう。
実務でどう使える?
ストレスチェック、健康診断結果など、
正規分布しない連続データにありがちな実務の現場でも大活躍です。
私自身産業保健関連の分析をお手伝いしたことがありますが、
Kruskal-Wallis検定には大変お世話になりました。
ANOVAより使用頻度が高かったです。
それだけ、Kruskal-Wallis検定はスーパーヒーローなのです。
Excelで実践!Kruskal-Wallis検定!!
早速、ExcelでKruskal-Wallis検定をやってみます。
3つの部署の体脂肪率を比較します。
今回ご登場いただくのは、マンホイットニーU検定の解説記事にも登場してくれた部署Aと部署B(勿論筋トレオタク・小林君も健在)です。
また、今回は筋トレが大ブームである部署Cにも登場していただきました。
今回のデータはこちらです。
| 部署 | 氏名 | 体脂肪率(%) |
| A部署 | A01 | 20.7 |
| A部署 | A02 | 19.8 |
| A部署 | A03 | 21 |
| A部署 | A04 | 22.3 |
| A部署 | A05 | 19.6 |
| A部署 | A06 | 19.6 |
| A部署 | A07 | 22.4 |
| A部署 | A08 | 21.2 |
| A部署 | A09 | 19.3 |
| A部署 | A10 | 20.8 |
| A部署 | A11 | 19.3 |
| A部署 | A12 | 19.3 |
| A部署 | A13 | 20.4 |
| A部署 | A14 | 17.1 |
| A部署 | A15 | 17.4 |
| B部署 | B01 | 26.6 |
| B部署 | B02 | 25.5 |
| B部署 | B03 | 28.8 |
| B部署 | B04 | 25.7 |
| B部署 | B05 | 24.5 |
| B部署 | B06 | 31.7 |
| B部署 | B07 | 27.4 |
| B部署 | B08 | 28.2 |
| B部署 | B09 | 24.4 |
| B部署 | B10 | 26.6 |
| B部署 | B11 | 28.3 |
| B部署 | B12 | 25.1 |
| B部署 | B13 | 28.9 |
| B部署 | B14 | 26.5 |
| B部署 | B15 | 27.3 |
| B部署 | B16 | 26.5 |
| B部署 | B17 | 32.6 |
| B部署 | B18 | 28 |
| B部署 | B19 | 25.4 |
| B部署 | 筋トレオタク・小林君 | 12 |
| C部署 | C01 | 10.7 |
| C部署 | C02 | 9.8 |
| C部署 | C03 | 11 |
| C部署 | C04 | 12.3 |
| C部署 | C05 | 9.6 |
| C部署 | C06 | 9.6 |
| C部署 | C07 | 12.4 |
| C部署 | C08 | 11.2 |
| C部署 | C09 | 9.3 |
| C部署 | C10 | 10.8 |
| C部署 | C11 | 9.3 |
| C部署 | C12 | 9.3 |
| C部署 | C13 | 10.4 |
| C部署 | C14 | 7.1 |
| C部署 | C15 | 7.4 |
1. 体脂肪率に順位をつける
=RANK.AVG([@体脂肪率(%)], 体脂肪率全体の範囲, 1)
で体脂肪率が低い順に順位がつけられます。
これを一番下のデータがあるセルまで繰り返します。
一つのセルに数式を入力したら、そのセルをクリックした後、セルの右下をダブルクリックすればすぐに一番下まで入力できます。

2. 順位を並べ替える
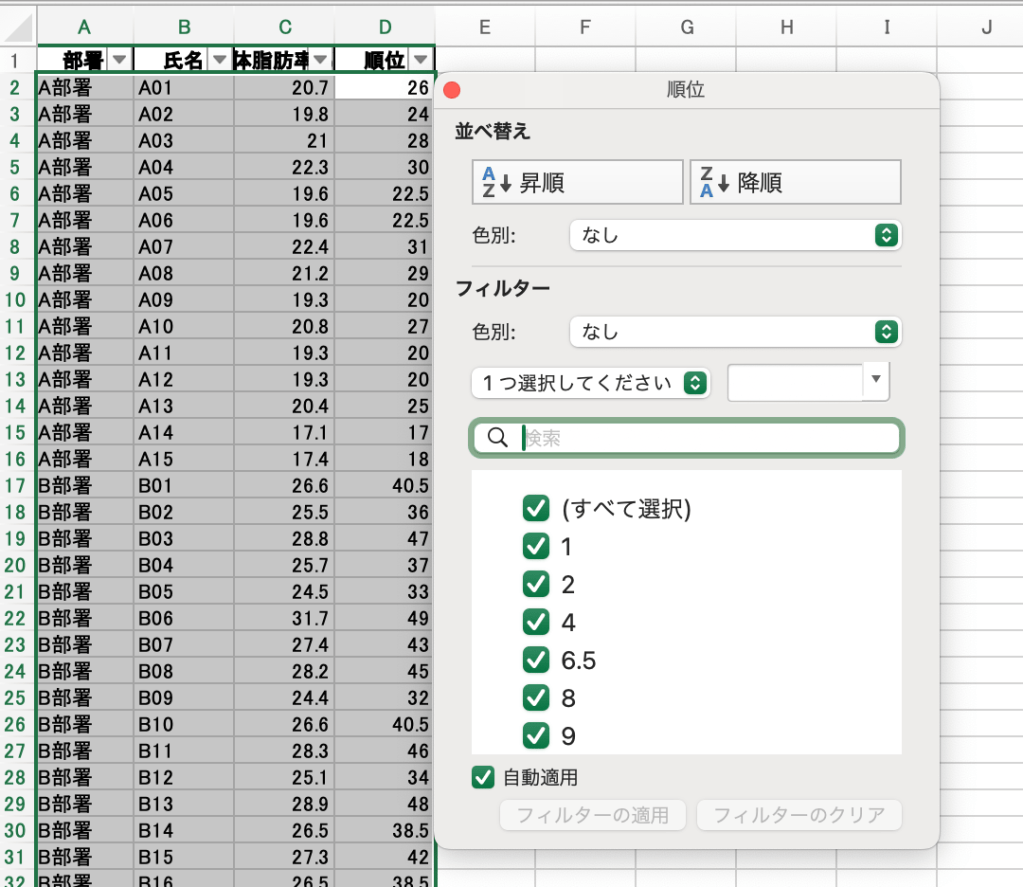
一番上の行を選択し、データ→フィルターをクリックします。

するとセルの右側に🔽が出るので、順位が表示されている場所の🔽をクリックします。
すると、並べ替え機能が表示されるため、「昇順」をクリックします。
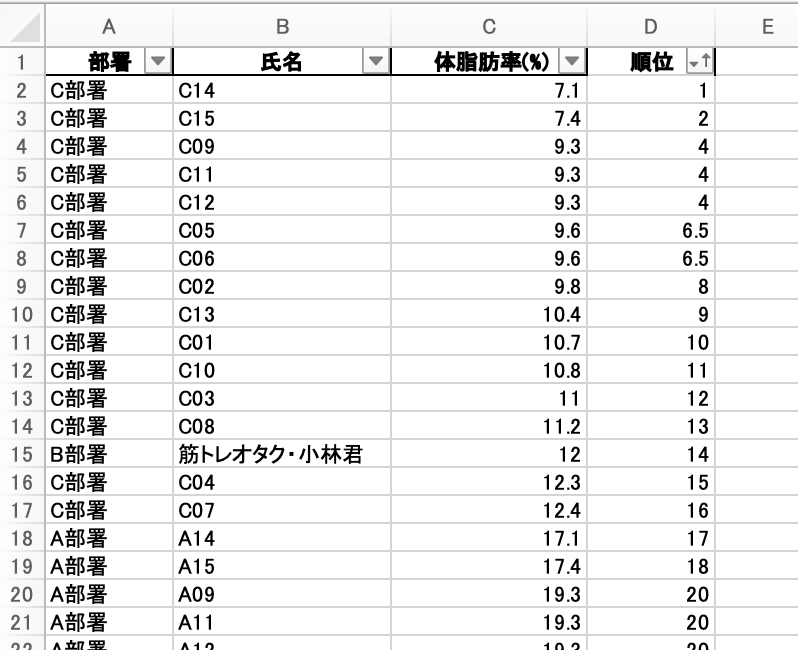
3. (同じ順位の人がいる場合)補正指数を求めるために、データを準備する
Kruskal-Wallis検定は「すべての値に順位をつける」ことで差を調べます。
でも、データの中に同じ値(=タイ=同順位になるデータ)があると、
順位の合計がズレて、検定統計量の精度が下がってしまうんです。
肝心の補正指数の求め方がこちら。
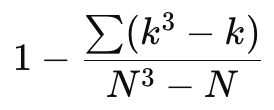
- k:同順位になっているデータの個数(タイのグループ単位)
- N:全体のデータ数
なんじゃこりゃ!!!
まあ落ち着いてください。順を追って説明します。
まず、「体脂肪率」が同じ人が何人いるかを調べるために、上のセルと比べながらカウントしています。(同値判定)
=IF([1つ上の人の体脂肪率]=[今の人の体脂肪率], [1つ上の人の同値判定]+1, 1)
と入力します。
これは、簡単に言うと「もし一つ上のセルの人の体脂肪率と本人の体脂肪率が同じだったら、同値判定に1を追加するよ。そうでなかったら1を表示するよ」という意味です。
つまり、同じ順位の人が何人いるかわかります。
これを一番下の人まで繰り返します。

次に、同じ順位になっているデータの個数(k)を求めます。
同値判定の右のセルに、
=IF(AND(OR([1つ下の同値判定]=1, [1つ下の同値判定]=””),NOT([今の同値判定=1])),[今の同値判定],””)
と入力します。
いきなり複雑になりましたね。
簡単に言うと、「同じ体脂肪率の人たちが並んでいて、その最後の行だけにk(人数)が表示されます。
これも一番下のセルまで行います。

そして、k3-kを求めるために、kの右のセルに、
=IF([今のk]=””,””,[今のk]^3-[今のk])
と入力します。
つまり、「kが空欄だったら何も表示しないよ、数値が入っていればk3-kを計算するよ」という意味です。

4. それぞれのグループの合計順位を求める
Kruskal-Wallis検定をするために、A部署・B部署・C部署それぞれの「順位の合計」を出します。
これを「順位和(じゅんいわ)」といいます。
これを求めるには、
=SUMIFS([順位が載っている範囲], [グループ名が載っている範囲], [グループ名])
と入力します。
つまり、指定したグループ名の順位だけカウントしてくれます。
他のグループも同様に行います。

5. それぞれの部署のデータの個数を求める
=COUNTIF([グループ名が載っている範囲], [グループ名])
を入力し、それぞれのグループのデータの個数を数えます。

6.検定統計量Tを求める
いよいよKruskal-Wallis検定の本体の値(=T)を出します!
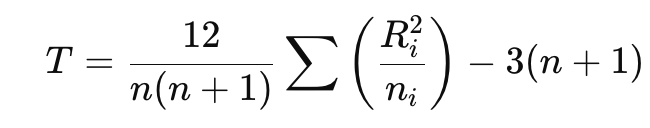
- Ri = 各グループの順位の合計
- ni = 各グループの人数
- n = 全体の合計人数(全てのグループの人数を足したもの)
よって、セルには
=(12/([個数全体]([個数全体]+1)))(([グループA合計順位]^2/[グループAデータ個数(人数)])+([グループB合計順位]]^2/[グループBデータ個数])+([グループCデータ合計順位]^2/[グループCデータ個数])-3*([個数全体]+1))
と入力します。
4つ以上比較する際は、+([グループCデータ合計順位]^2/[グループCデータ個数])の後ろに+([グループDデータ合計順位]^2/[グループDデータ個数]),+([グループEデータ合計順位]^2/[グループEデータ個数])…と追加してください。

7. (同じ順位のデータがある場合)補正指数を求め、補正したT(T’)を求める
再度、補正指数の式をお見せします。
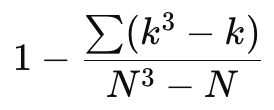
- k:同順位になっているデータの個数(タイのグループ単位)
- N:全体のデータ数
補正指数は、
=1-SUM([k3-kのデータがある範囲])/([個数全体]^3-[個数全体])
で求めます。
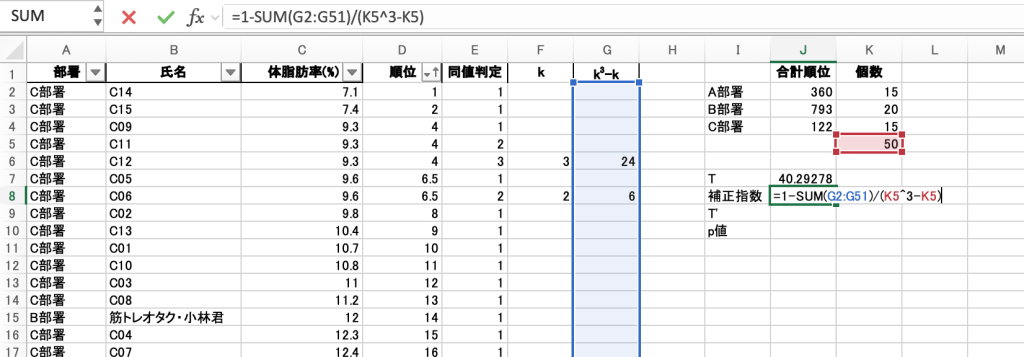
そして、T’ = T/補正指数で求めます。

8. p値を求める
T(またはT’)はΧ2分布に従うのでCHISQ.DIST.RT関数を用いて計算します。
セルには、
=CHISQ.DIST.RT([TまたはT’],[自由度])
と入力します。
自由度は、グループ数-1で求められます。

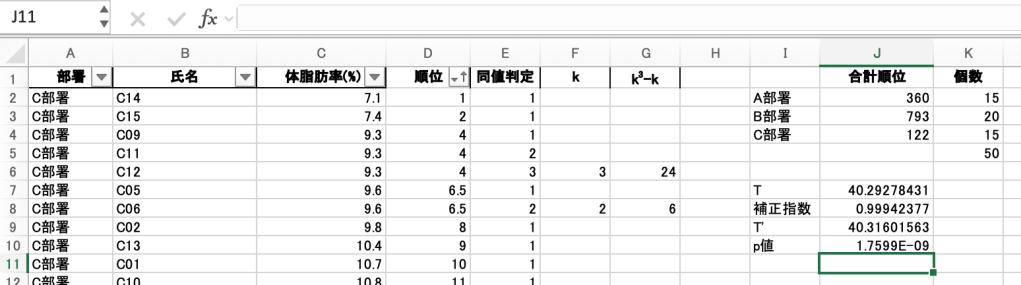
求められたp値、1.7599E-09とは、1.7599 × 10⁻9のことです。
つまり、0.05より小さいため、統計学的に有意と考えられます。
「A部署とB部署とC部署のどこかに有意な差があるぞ!!」ということです。
まとめ
Kruskal-Wallis検定は、
- 3つ以上のグループ
- 正規分布していない
- 順位で比較したい!
時に頼れる検定です。
困った時はKruskal-Wallis検定に甘えちゃいましょう。
おまけ PythonでKruskal-Wallis検定をやってみた
さーて、お待ちかね(?)のPythonコーナーです。
先ほどと同じデータでKruskal-Wallis検定を行います。
勿論「Pythonなんか使わないよ!!」という方はこの先を読まなくてもOKですが、
使いこなせるとExcelで分析するよりも早くて正確な結果が出ます。
import pandas as pd
from collections import Counter
from scipy.stats import kruskal, chi2
# データ読み込み
df = pd.read_excel("パス名")
# Kruskal-Wallis検定(通常)
groups = df.groupby("部署")["体脂肪率(%)"].apply(list)
stat, p_original = kruskal(*groups)
# タイ(同値)があるかチェック
counts = Counter(df["体脂肪率(%)"])
ties_exist = any(v > 1 for v in counts.values())
# 全体のデータ数
N = len(df)
if ties_exist:
# 補正指数 C を計算
sum_k3_k = sum(k**3 - k for k in counts.values() if k > 1)
correction_C = 1 - (sum_k3_k / (N**3 - N))
# 補正後の統計量 T′
stat_corrected = stat / correction_C
# 群数 - 1(自由度)
dfree = df["部署"].nunique() - 1
# 補正後のp値
p_corrected = chi2.sf(stat_corrected, df=dfree)
print("タイ(同値)が見つかったため、補正を適用しました。")
print(f"補正指数 C: {correction_C:.6f}")
print(f"補正後のT値: {stat_corrected:.4f}")
print(f"p値(補正あり): {p_corrected:.10f}")
else:
print("タイ(同値)はなかったため、通常のKruskal-Wallis検定を使用します。")
print(f"T値: {stat:.4f}")
print(f"p値(通常): {p_original:.10f}")
出力結果:
タイ(同値)が見つかったため、補正を適用しました。
補正指数 C: 0.999424
補正後のT値: 40.3393
p値(補正あり): 0.0000000017
