統計と現場の狭間で今日も生きる保健師の皆さん、実習や講義に追われている看護学生の皆さん、こんにちは。
突然ですが、こんな経験ありませんか?
「保健指導したけど…あの人、本当に変わったのかなぁ…?」
食べたものを記録してくれてはいるけど、なんかうさんくさい。
体重は減ったけど、寝不足のせいじゃないか疑惑アリ。
そんな時に数値の変化をガチで検証してくれるのが……
Wilcoxon検定(ウィルコクソン)です。
Wilcoxon検定って何者なんじゃ?
簡単に言うと、
同じ人の“ビフォーアフター”データを比べて、差があるかどうか検定する方法です。
劇的!ビフォーアフターみたいなものです。なんということでしょう!!
でもただの差じゃなくて、
「順番に注目したノンパラメトリック検定」なんです。
つまり…
- 正規分布? → 気にしません!
- 外れ値? → あってもある程度は耐える!
- 平均じゃなくて順番で勝負!
そう、Wilcoxon検定はデータの現実を受け止める、強くて優しい検定なんです。
こんな場面で使えるよ⭐︎
- 健康教室前後のBMIを比較
- ストレススコアの改善チェック
- 睡眠時間の変化確認
などといった場面で使えます。
t検定とどう違うねん!!
「ビフォーアフターなら、対応のあるt検定じゃないの?」
そう思った方、鋭い!!
でもWilcoxon検定は、
「t検定を信じてたけど、分布が正規じゃないと気づいた時の救世主」です。
平均ではなく順位で勝負!!
といった特徴があります。
やっぱり注意事項はあるよ。
1. 2群比較にしか使えない
- 対象は「2条件のみ」です。
- 例:介入前と介入後の比較はOK。でも、介入前・後・3ヶ月後の3点比較はできません(その場合はFriedman検定などが必要!)。
2. 検定対象が「差の符号と順位」なので、情報が捨てられる
- Wilcoxon検定は差を数値として扱うのではなく、差の絶対値の「順位」とその符号(+/−)だけを使います。
- データの細かい情報を無視します。
(例えば「5.0と5.1の差」と「5.0と9.0の差」が同じ扱いになる)
3. 外れ値が多い場合や差がない場合の扱いに弱い
- 差が0のペア(全く変化していない)は、検定から除外されます。
例として、BMIが前後とも25.0だった人は「データとしてノーカウント」。 - 外れ値はノンパラなので耐性はありますが、多すぎると結果の信頼性が下がります。オーノー!!
4. サンプルサイズが小さいと有意になりにくい
- データが少ないと「変化はありそうなのに有意差が出ない」ことがあります。
5. データの「対」になっていないと使えない
- データは必ず同じ人・同じ対象で2回測ったペアデータでなければいけません。
- 対応が取れていない(例えば「別々の人の前後比較」)と使えません。
つまり、Wilcoxon検定は「相手の変化には気づくけど、どれくらい変わったかまではあまり聞かない、奥ゆかしい人」です。
黒髪の人が暗めの茶髪になろうが、ブリーチを3回した金髪になろうが、「変わったね」くらいしかコメントしてくれません。
正確だけど慎重派。だから、たまに見逃しもあるんです。
弱点をカバーするには?
- サンプルサイズを多めに確保する!!
- 分布が明らかに正規なら、対応のあるt検定の方がよい場合もある!
- 3条件以上で比較したいなら、Friedman検定へバトンタッチ
実際にWilcoxon検定をExcelでやってみよう。でも結構手間だぞ。
ではでは、いつも通り今回のWilcoxon検定の対象者の皆さんに出て来てもらいましょう。
※今回ご紹介するのは近似値を求める方法です。悪しからず。
体重を減らすために保健指導を受けた方々です。カモォ〜〜〜〜ン!!
| ID | 指導前体重(kg) | 指導後体重(kg) |
|---|---|---|
| A | 72.0 | 65.0 |
| B | 85.2 | 83.1 |
| C | 60.3 | 58.4 |
| D | 90.0 | 92.1 |
| E | 70.5 | 65.3 |
| F | 55.0 | 55.0 |
| G | 80.8 | 74.6 |
| H | 78.0 | 78.0 |
| I | 65.2 | 60.2 |
| J | 67.8 | 66.9 |
- 指導前と後の差を求める
同じ人の指導後-指導前の体重を引きます。
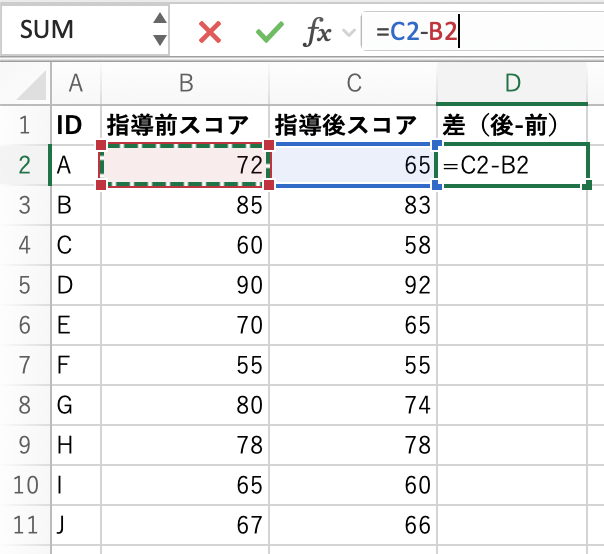

- 他の人たちも同じように計算します。
先ほど計算したセルの右下をダブルクリックすると、下まで勝手に計算してくれるので便利です。

- 差が「0」だった人のデータは検定から除外します。
今回のデータだとFさんとHさんが除外対象です。
Fさん!Hさん!……短い間!!! くそお世話になりました!!!


- 絶対値を求める
ABS関数を使って絶対値を求めます。
今回は、=ROUND(ABS(指定セル),1)と入力することで、「指定セルの絶対値を求めるよ、小数第二位で四捨五入して、小数第一位まで表示するよ」と指示しています。
一番上の計算が終わったら差が0の人以外の絶対値を求めるのを忘れずに。


Q. なぜROUND関数(四捨五入)も使うの?
A. ABS関数は絶対値を求めてくれますが、Excelの仕様上、一見小数が正しく表示されていても2.1000000000000018…..といった極めてわずかなズレを含んだ数になることがあります。
これでは同じ値のはずの人が違う値だと認識されます。
なので、ROUND関数で四捨五入してしまえば後に「見かけ上は同じ値のはずなのに順位が違う…」という事態を防げるのです。
めんどくせぇ
- 順位を求める
RANK.AVG関数で順位を求めます。
RANK.AVG関数を使って順位を付けると、
同じ値(絶対値)が複数ある場合は、「その順位の平均値」が自動で割り当てられます。
今回の例だと、
BさんとDさんの絶対値がどちらも 2.1 で並んでいます。
このとき、順位で見ると 本来なら3位と4位になるはずですが、同点なので、
(3 + 4)÷ 2 = 3.5
と計算され、どちらも「3.5位」となります。
これがRANK.AVGの動き方です。
今回の場合だと、=RANK.AVG(指定セル,指定範囲,1)と入力しているため、
「指定セルが指定範囲の中で何位かを求めるよ、小さい値ほど1位に近づくよ(昇順)」という意味です。
尚、ここで=RANK.AVG(指定セル,指定範囲,0)としないでください。
これだと順位の付け方が降順になり、後に求める検定統計量やp値が誤った結果になります。


- 順位に符号をつける
指導後-指導前の差と順位の符号が一致するようにします。
(例として、差が-7であれば順位に-をつける。差が2.1であれば順位に符号をつけずそのままにする)
手作業でもOKですが、IF関数を使った方が楽で正確です。
=IF(差の値のセル>0, 順位のセル, -順位のセル)で簡単に求められます。
これは、「差の値のセルが0より大きければ、順位にマイナスの符号はつけないよ。でも0より小さければ順位にマイナスの符号をつけるよ」と言う意味です。

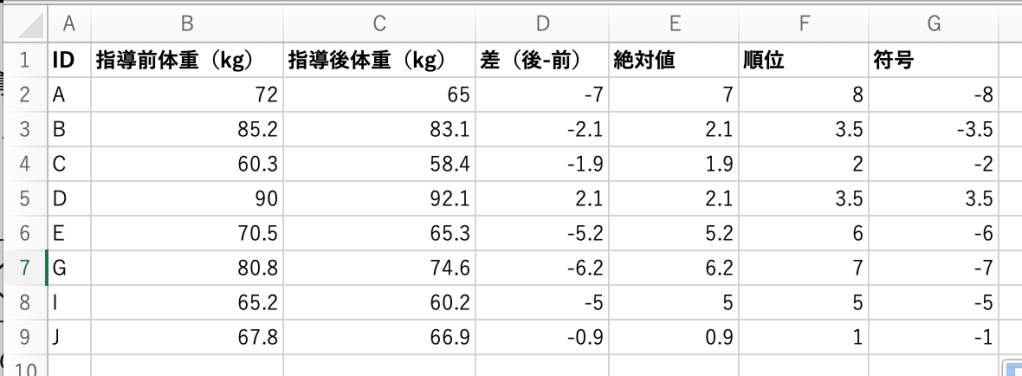
- 符号付き順位(または順位)を二乗する
=符号のセル^2と入力すれば、二乗した値が求められます。


- 符号付き順位、二乗した順位の合計をそれぞれ求める
SUM関数を使ってしまえば楽です。

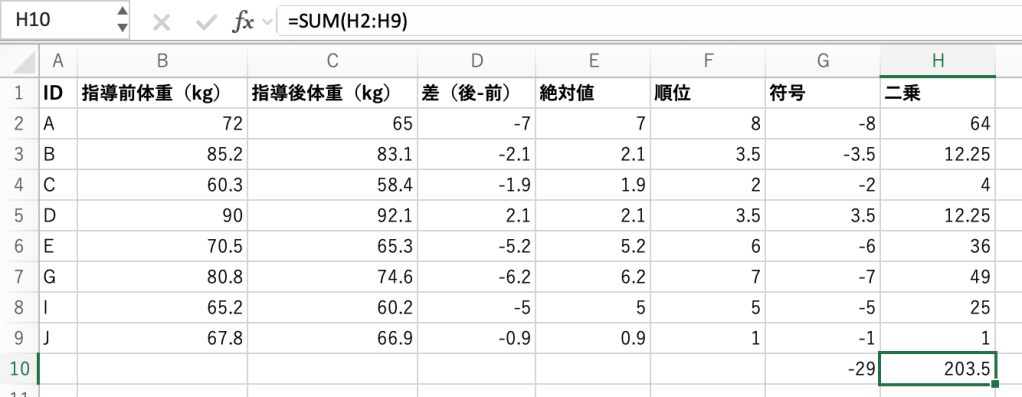
- (符号付き順位の合計がプラスの場合)マイナスにする
今回の例では不要ですが、もし符号付きの順位の合計がプラスになった場合は、マイナスをつけた値を別セルに入力してください。
下記のようにIF関数を使ってもOKです。(ちょっとめんどいけど)

- 検定統計量(Z値)を求める
=(マイナス付き符号付き順位合計セル)/SQRT(二乗の合計セル)で求めます。


- p値を求める
=NORMDIST(検定統計量セル)*2で求められます。
NORMDIST関数は、簡単に言えば検定統計量がどれくらい極端かを示してくれます。


今回のp値は0.042062733でした。
有意水準の0.05を下回っているので、今回の結果は偶然ではないよ、ということを示しています。
今回の結果は大多数の方が体重が減っているため、保健師さんとしては嬉しい結果ですね。
まとめ
今回はFriedman検定について紹介いたしました。
Friedman検定は介入前後のビフォーアフターを調べる検定でしたね。
「なんということでしょう!!」という素晴らしい結果が出なかったとしても、皆さんなら諦めずに前に進んでくれると信じていますよ。
結果が出なくても焦らないで。あなたの頑張りを見てくれる人は絶対どこかにいますから。
できる!できる!君ならできる!!
今日から君は!!!!太陽だ!!!!!!
おまけ:Pythonでやってみた
Excelでは統計量とp値を求めるのに一苦労(しかも近似値しか出ない)でしたが、今度はPythonで一気に求めちゃいます。
import pandas as pd
import numpy as np
from scipy.stats import wilcoxon
from math import sqrt
# Excelファイルの読み込み
df = pd.read_excel("データのパス名")
# 指導前後の体重データを抽出
before = df["指導前体重(kg)"]
after = df["指導後体重(kg)"]
# 差を計算し、差が0でないものにしぼる(Wilcoxonの前提)
diff = after - before
nonzero_mask = diff != 0
before_filtered = before[nonzero_mask]
after_filtered = after[nonzero_mask]
n = len(before_filtered)
# Wilcoxon検定(両側)
stat, p = wilcoxon(after_filtered, before_filtered, alternative='two-sided')
# 結果出力
print(f"T値(統計量): {stat}")
print(f"p値(両側): {p:.4f}")
出力:
T値(統計量): 3.0
p値(両側): 0.0391
