今回は、統計で使われている数式（正規分布・二項分布・t分布）を紐解いていきます。

「数学？？私とっくの昔に挫折したんですけど〜〜そもそも数式まで勉強する必要ある？？」という方、確かに看護学生・保健師として検定をする分には、検定の知識さえあればデータ分析はできるでしょう。

しかし、数式を知ることにより、検定で何をしているかが深く理解しやすくなります。
研究・論文を発表する時、根拠を詳しく説明できるようになるのです。

数学が苦手だった方、得意だったけど忘れた…という方、ご安心ください。
もちろん文系だった方も大丈夫です。
私もこの統計数学を勉強し始めた時は意味が分からず挫けそうになりました。
そのため、この記事では数式を詳しく分解し、何をやっているかを説明します。

---

正規分布

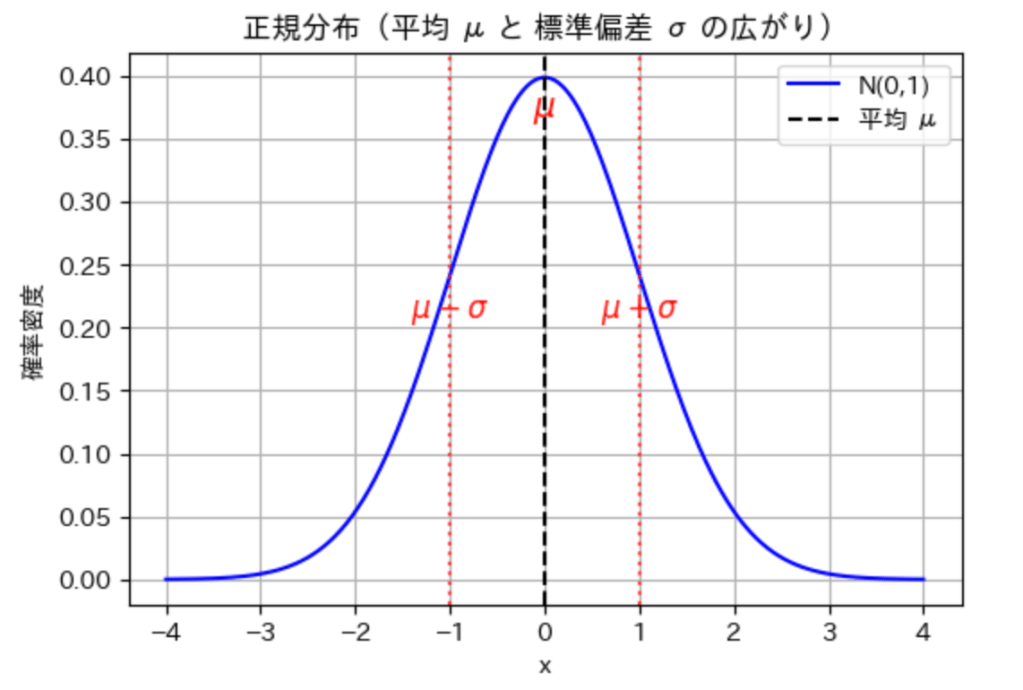
式（確率密度）

• 登場人物
  • μ（ミュー）：山の中心（平均）の位置
  • σ（シグマ）：山の広がり（標準偏差）
  • exp⁡(⋅)：e をその中身だけべき乗（同じ数を自身に何度も掛け合わせ）したもの。
  • π：円周率（3.1415…）
• 形づくる部分：
  平均から離れるほど二乗でペナルティ → 山の中心が高く、離れると素早く小さくなる。
• 大きさを合わせる定数：
  面積（合計の確率）が1になるように高さを調整する係数。
• 直感
  「たくさんの小さな偶然が積み重なる量」はこの形になりやすい（テストの点数、身長など）。

---

二項分布

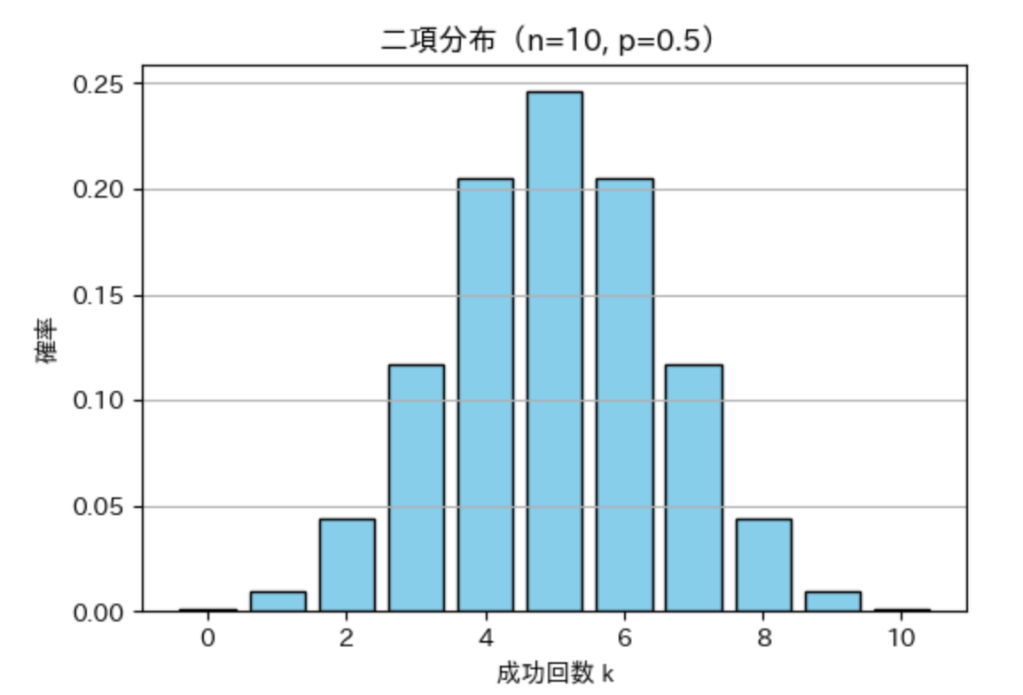
コイン投げの「表が何回出た？」のように、成功回数を扱います。

式（確率質量関数：PMF）

• 登場人物
  • n：試行回数（例：コインを何回投げるか）
  • p：1回で成功する確率（例：表が出る確率）
  • k：成功回数
  • （組合せ）=
    （階乗）：m×(m−1)×⋯×1
• 形づくる部分：
  特定の並び方1通りに注目したときの確率。成功が k 回、失敗が n−k回起きる確率。
• 大きさを合わせる部分（というより数え上げ）：
  その並び方が何通りあるかを掛ける（位置の入れ替えの数）。

---

t分布

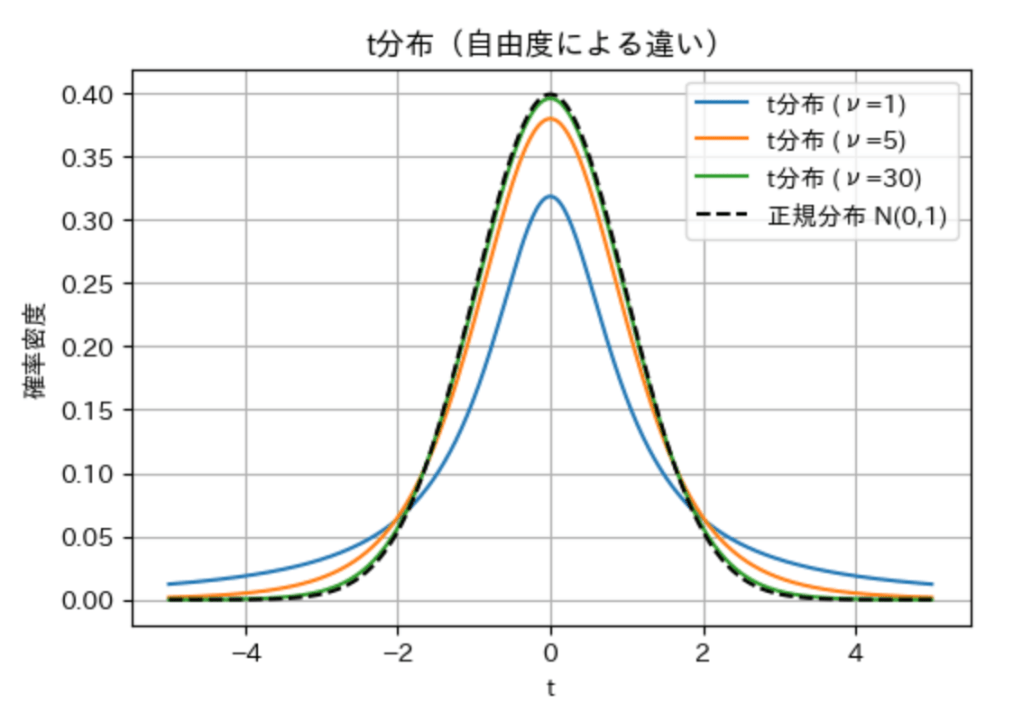
平均0の左右対称の山。標準偏差がはっきり分からないときに現れやすい。標本が小さいと特に使う。

式（確率密度）

• 登場人物
  • ν（ニュー）：自由度（だいたい「データの数−1」くらいのイメージ）
  • Γ(⋅)（ガンマ関数）：階乗の概念を複素数まで拡張したもの。意味が分からないと思いますが、ひとまず「グラフ面積を1に調整するためのもの」と考えてもらえればOKです。
    整数 m に対して 
• 形づくる部分：
  正規分布の式に似た「山を作る係」。
  端（大きい |t|）でもゼロになりにくい → 裾が太い（外れ値に強い）。
• 大きさを合わせる定数：
  面積が1になるように高さ調整。見た目は難しいけれど「正規化のための定数」と思えばOK。
• 直感
  • νが小さい（データが少ない）ほど裾が太い＝不確かさが大きい。
  • νが大きくなると正規分布に近づく（推定が安定してくる）。