突然ですが、あなたは「この村に住む1000人の平均身長を知りたい!」と思ったことはありますか?
え?そんなの思ったことはない?困ったなぁ…
村に住む1000人全員の身長を測るのはとても大変ですよね。
そこで役に立つのが統計学です。
一部の人を調べるだけで、村全体の平均を予測できるんです。
今回はその方法を「点推定」「区間推定」、さらに「対数尤度(「たいすいゆうど」と読みます)」と「ベイズ推定」まで、やさしく紹介します!
点推定(まずは1つの数字で予想)
1000人の村から100人をランダムに選んで測ってみたら、平均は 160cm でした。
「ほほう…それなら村全体の平均も160cmだな!」
そう、この考え方が点推定です。
ただし、選んだ100人の集まり方によって結果がブレる可能性があります。
例えば、偶然身長が高い人ばかり100人集まった可能性も否定できません。
しかし、得られたデータだけから計算可能なので、お手軽です。これは大きなメリットですね。
点推定の数式はこちら。
登場人物:
つまり「調べた人数で割った平均 = 村全体の平均の予想値」という意味です。
区間推定(幅を持たせた安心感)
点推定だけだと心もとないので、「幅を持たせた予想」をします。
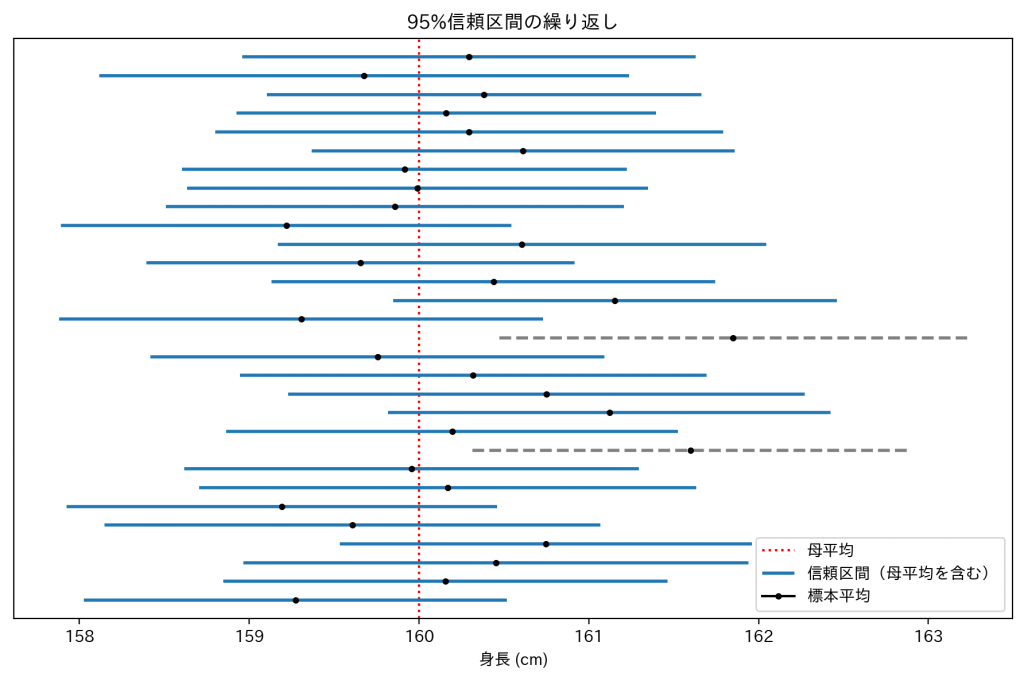
この「幅を持たせた予想」を、信頼区間(Confidence Interval) と呼びます。
たとえば「村の平均身長は95%の確率で158〜162cmの間にある」というのではなく、
「もし何度も100人をランダムに測って区間を作れば、その95%が本当の平均を含む」 という意味になります。
(ここが後述するベイズの「信用区間」との大きな違いです。ベイズでは「この範囲にある確率が95%」と言えるのです。)
この信頼区間の仕組みを使ったのが区間推定です。
信頼区間は「毎回の推測は少しブレるけど、その95%は本当の答えを捕まえられる網」のようなイメージです。
図式化すると、このようになります。
数式はこちら。
登場人物:
つまり「標本平均 ± 誤差」で、「村の平均はこの範囲にありそう!」 と示せます。
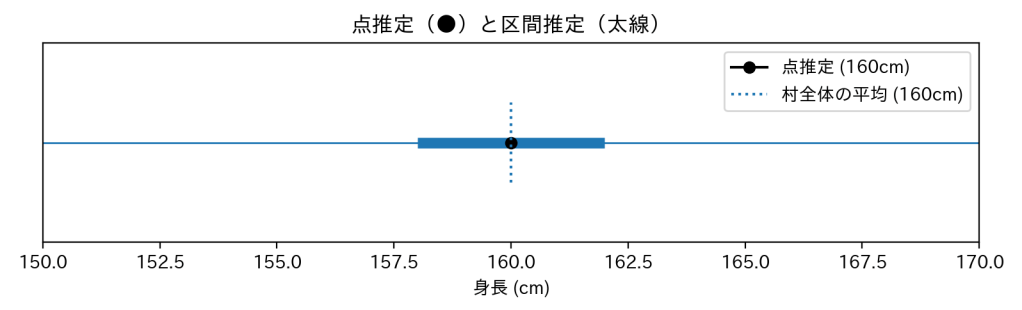
では、これまでで点推定と区間推定を学んだので、図にしてみました。
点と区間の意味がこれでイメージしやすくなると思います。
対数尤度(一番もっともらしい数字を探す)
データから「どの平均が一番それっぽいか?」を調べるのが尤度で、
計算をラクにするために「対数」をとったものが対数尤度です。
イメージ:
- 平均160cmと仮定したら、データにすごく合う。
- 平均150cmと仮定したら、ちょっと合わない。
グラフにすると山の形になり、山の頂上が「最尤推定値(点推定の一種)」です。
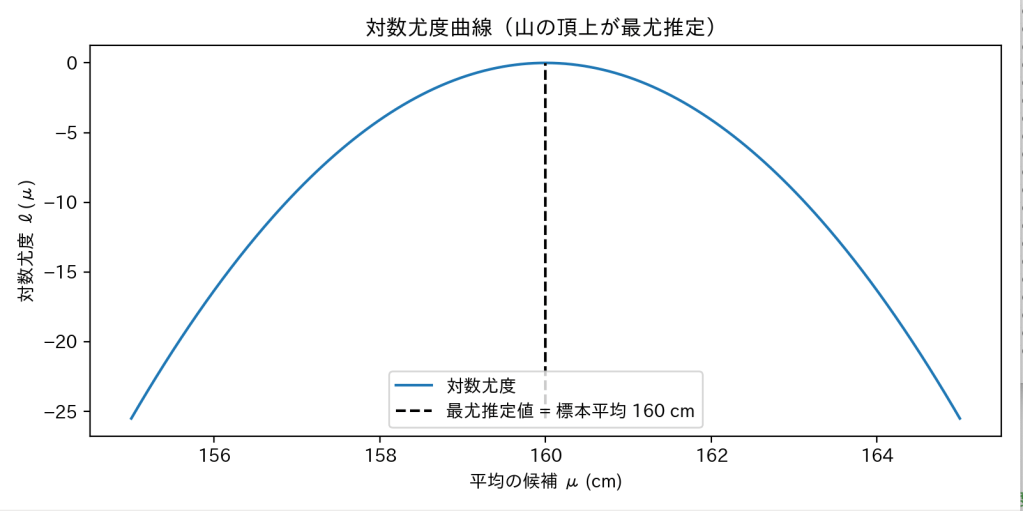
※確率は 0〜1 の間にあるので、対数を取るとどうしても 0 以下になります。でも大事なのは「どの μ(母平均) のときに一番大きな値を取るか」で、それが最尤推定値です。
数式はこちら。
登場人物:
のときの対数尤度」
だとしたときに、データ
が出る確率」
つまり、「この平均が一番もっともらしいかどうかを計算するための式」です。
頂上が一番高いところ(最尤推定値)が「これだ!」という点推定になります。
※ここでは分布を正規分布と仮定しているので、最尤推定値は標本平均になります。他の分布(指数分布など)だと別の式になることもあります(後述)。
正規分布VS指数分布の対数尤度
正規分布の場合
確率密度関数
これは「平均が μ の正規分布」の形を表す式です。
ここでいう μ は 村全員の平均身長(母平均)の候補 です。σ² は広がり(ばらつき)を表します。
正規分布については、「中学生でも分かる!?統計数学〜正規分布・二項分布・t分布〜」で詳しく説明していますので、よろしければこちらもどうぞ。
尤度関数
よく分からない記号が出ましたね(私だけか?)。
登場人物を紹介します。
:個別の確率(1人分)
→これは「データxi(i番目の人の身長)が、平均 μ の正規分布から出る確率の大きさ」を表しています。:全員分の掛け算
→この「Π(パイ)」記号は「全部掛け算する」という意味です。
つまり、N人分の「もっともらしさ」をまとめて掛け算しています。:尤度
→この掛け算の結果が「尤度」と呼ばれます。
つまり「もし平均が μ だとしたら、N人分のデータがそろって出る確率の大きさ」です。
つまりこれは、N人分のデータをもとに、「もし本当の平均が μ だとしたら、このデータが出る確率はどのくらいか?」を表しています。
μ の候補ごとに「もっともらしさ」を比べる道具です。
対数尤度
先ほどの尤度関数の式は掛け算だらけでカオスでしたね。
そこで、対数を取って足し算に変えています。
式の形から、μ がデータに近いほど値が大きく(0に近く)なり、遠いと小さく(よりマイナスに)なります。
グラフにすると山のような形になり、頂上が「一番もっともらしい平均」になります。
登場人物:
:「データと平均 μ のズレ(二乗)の合計」
:ズレが大きいと値が小さくなる(マイナス方向へ動く)
:定数(μには関係しないので無視できる)
:全体の対数尤度。山型のグラフになり、頂上が「一番もっともらしい μ(最尤推定値)」になる
「え、最初に教わった対数尤度の式と違うじゃん!?」と思った方もいるかもしれません。鋭い!
実は最初の式は「どんな分布でも使える一般形」で、この式は「正規分布に当てはめて整理したもの」です。
だから内容は同じで、書き方が違うだけなんです。
最尤推定値(MLE)
計算すると「標本平均(データの平均)」が μ の最尤推定値になります。
つまり「100人を測った平均=村全員の平均のもっともらしい推定値」だ、ということです。
指数分布の場合
確率密度関数
これは「待ち時間」や「電球の寿命」などを表すのによく使う指数分布です。
θ(シータ)は「レート(率)」と呼ばれるパラメータで、大きいと平均は小さくなります。平均は 1/θ です。
つまり、
- θ が大きい → 平均が小さくなる → すぐに出来事が起きやすい
- θ が小さい → 平均が大きくなる → 出来事がなかなか起きない
例として、バス停でバスが来るまでの時間が指数分布に従うとすると、
- θ=0.2なら → 平均待ち時間は 1/0.2=5 分
- θ=0.5 なら → 平均待ち時間は 1/0.5=2 分(もっと早く来る)
尤度関数
これも同じく、「θ を仮定したときに、このデータが出る確率の大きさ」を表しています。
ただし正規分布とは掛け算の中身が異なっています。
ここでも登場人物を見ていきましょう。
:1人分(1回分)のもっともらしさ
:N人分をまとめて掛け算する記号
:全体として「もしレートが θ なら、このデータが出るもっともらしさ」
対数尤度
ここでも掛け算を対数に変えて足し算にしています。
θ を大きくしたり小さくしたりしていくと、どこで「一番もっともらしいか」が分かるようになります。
登場人物:
:「θ の対数」を N 個分足したもの
:データを全部足した合計
:データの合計に θ を掛けたマイナスの項
:全体の「対数尤度」。θ を動かしていくと山の形になり、頂上が「一番もっともらしい θ(最尤推定値)」になる
最尤推定値(MLE)
計算してみると、指数分布の場合は 標本平均の逆数 が最尤推定値になります。
つまり「データの平均が大きいと θ は小さくなり、データの平均が小さいと θ は大きくなる」という関係になります。
※指数分布のパラメータは、教科書によって λ(ラムダ)と書かれることが多いですが、ここでは「パラメータ一般」を表す記号 θ(シータ)を使っています。意味は同じです。
正規分布VS指数分布の対数尤度まとめ
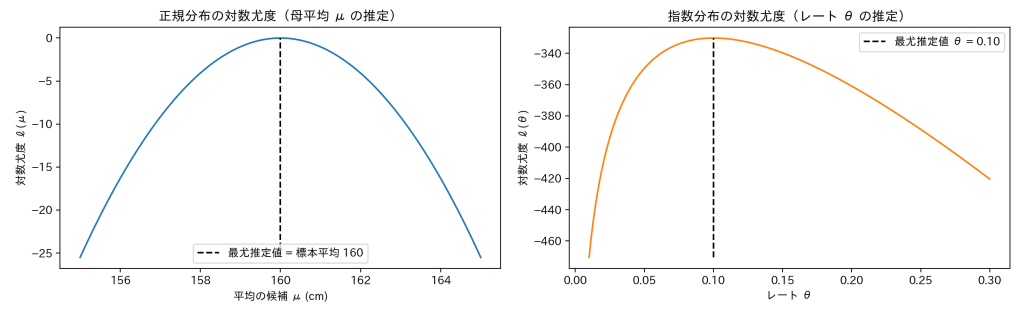
- 正規分布のとき → 「データの平均そのもの」が答え
- 指数分布のとき → 「データの平均をひっくり返した(逆数をとった)もの」が答え
分布の種類が違うと、同じ「最尤推定」という方法でも答えが変わるんだよ、というのがポイントです。
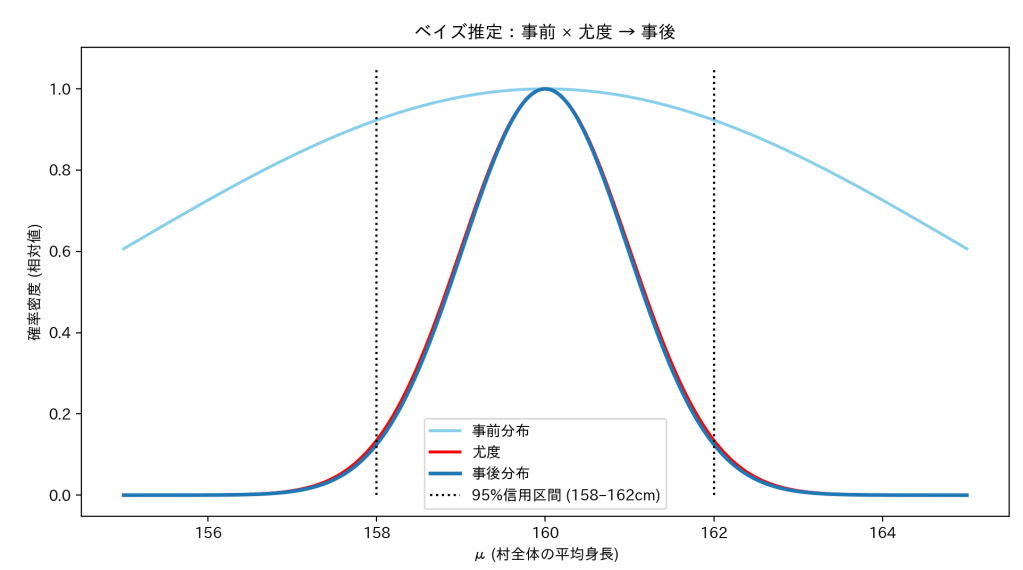
ベイズ推定(過去の情報も活用)
ここで「去年の村のデータ」があったとしましょう。
去年は平均が 155〜165cm の間にありそうだった。
今年の100人分のデータ(160cm)と、去年の情報を組み合わせると、
「今年の平均はだいたい 158〜162cm の確率が高い」と言える。
これがベイズ推定です。
幅を示すときには「信用区間(Credible Interval)」と呼びます。
ここで出てきた「158〜162cm」という数字は、信頼区間でも同じ幅になることがありますが、解釈の仕方が違う点がポイントです。
ベイズ推定の式はこちら。
登場人物:
「100人のデータDを測ったあと、村全体の平均身長(θ)がどんな値かの確率」
→事後分布(答え)
「もし平均身長がθだったら、100人のデータが出る確率」
→尤度(データのもっともらしさ)
「データを測る前の予想。去年の村のデータから155〜165cmくらいと考えていた」
→ 事前分布(スタート地点の信念)
「データDが観測される確率」
→ 調整用の定数(確率の合計を1にするためのもの)
少しややこしくなってきましたね。
要するに、
- 去年までの経験で「村の平均身長は155〜165cmくらいだろう」と思っていた(事前分布)。
- 今年、100人を測って平均が160cmだった(データD)。
- じゃあその結果を踏まえて「村全体の平均は158〜162cmくらいだろう」と更新する(事後分布)。
ベイズ推定は「予想(事前分布)+データ(尤度)=更新された予想(事後分布)」という流れで考えます。
おまけ:信用区間
ベイズ推定から得られる「事後分布」を使って、
「村の平均身長はこの範囲にある確率が95%」という区間を求められます。
式はこちら。
登場人物:
→ ここでは「100人を測ったデータを踏まえて」という意味
→ 例:158cm ≤ θ ≤ 162cm= 0.95:その範囲に入る確率が95%
→ つまり「95%の自信を持って、この範囲に村の平均があると言える」
ベイズ推定で求めた事後分布から、
「村の平均身長は158〜162cmの間にある確率が95%です」
と言えるのが 信用区間です。
→信頼区間と違い、信用区間は 「この範囲にある確率が○%」と直接言える のがポイントです!
関係性まとめ
- 点推定 :「村の平均は160cmだ!」
- 区間推定 : 「158〜162cmの間にあるはず」
- 対数尤度 :「データに一番フィットするのは160cmだ」と計算で探す
- ベイズ推定 : 「去年の情報も合わせると、158〜162cmくらいが確率高い」
これらを別の言い方にすると、
- 点推定:的に矢を1本刺す
- 区間推定:的の中心を大きく囲う
- 対数尤度:「矢がどこに当たると一番もっとも(尤も)らしいか」を数値で計算
- ベイズ推定 :「過去の経験」も参考に矢が当たりやすい場所を探す
全体まとめ
1000人の村の平均身長を調べるのは大変です。
でも統計を使えば、
- 一部の人だけで「予想」できる(点推定)
- 幅を持たせて「安心」できる(区間推定)
- 一番データに合う値を数式で探せる(対数尤度)
- 過去の知識も合わせて「確率」で考えられる(ベイズ推定)
と現実的に数値を扱えるようになります。
この概念が分かると集団の状態を捉えやすくなるため、この記事を読んだのをきっかけに理解しちゃいましょう!
