今回は「カイ二乗分布」と「F分布」の数式について説明していきます!
ちょっと難しく感じるかもしれませんが、これらは元をたどれば「正規分布」から派生した仲間達なのです。
過去の記事と組み合わせて読むとより理解が深まると思います。
是非読んでください!!
過去記事:
カイ二乗分布
特徴
- 値は 0 以上しか取らない
- グラフは右に長い裾を持つ(非対称)
- 自由度が大きくなると正規分布に近づく
- カイ二乗検定に使われる
「そもそもカイ二乗検定って何だったっけ?」という方はこちらの記事をご参照ください。
「自由度」という言葉に馴染みがない方もいらっしゃると思うので、後述します。
自由度って?
「自由度」とは、データの中で「自由に動ける数字の数」 のことです。
例:3人のテストの平均点が60点だと決まっているとします。
- 1人目と2人目の点数を決めたら、3人目は自動的に決まってしまいます。
→このとき「自由に決められるのは2人分」なので、自由度は 2 です。
t分布のように平均を使う場合、自由度は「データの数 − 1」になります。
しかし、今回のカイ二乗分布では「足した正規分布の数」が自由度になります。
簡単にまとめると、
- 自由度 = 「自由に決められるデータの数」
- 平均を計算するときは1つ制約があるため
- カイ二乗分布では「足した数そのもの」が自由度になる
定義
もし次のような正規分布に従うデータを考えます:
これらを二乗して足すと…
この が従う分布を カイ二乗分布(自由度 k) と呼びます。
確率密度関数
登場人物:
:自由度(足した正規分布の数)
:自由度によって形が変わる部分
:右に長く尾を引く形をつくる
:ガンマ関数。階乗をもっと広い数(整数以外や小数)にまで拡張したもの
図式化するとこちら。
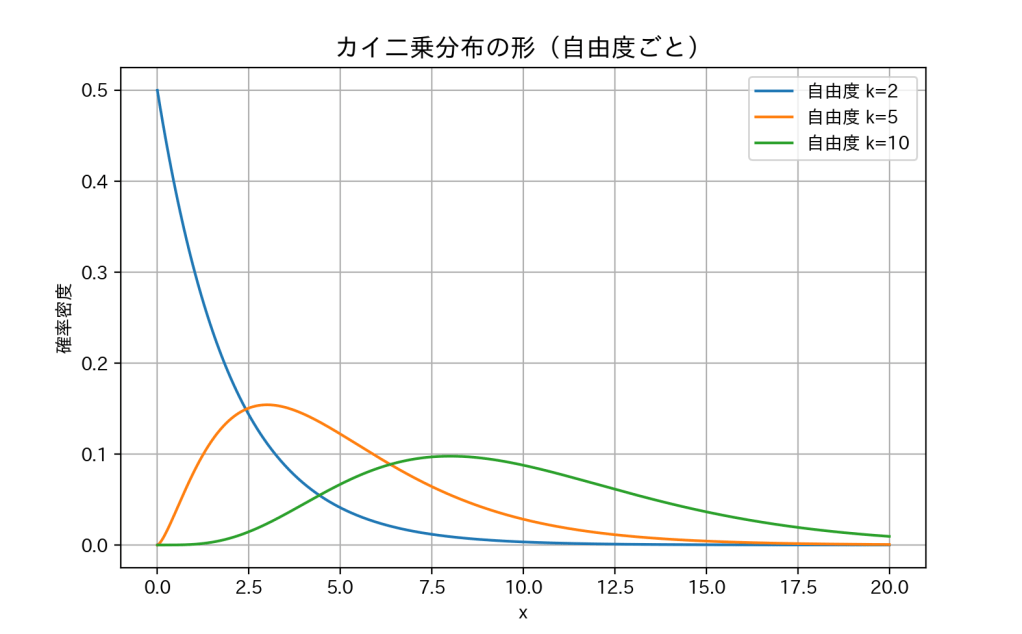
自由度が小さいと「山は左(0の近く)に寄り、右に長い裾を引く形」になっていますね。
一方、自由度が大きくなるとまるで正規分布のような形に近づきます。
F分布
特徴
- 値は 0 以上
- グラフは右に長い裾を持つ
- ANOVA(分散分析)に使われる
- 「分散どうしの比」を調べるときの分布
「ANOVAって何だか忘れっちまった…」という方はこちらの記事をどうぞ。
定義
2つの独立したカイ二乗分布 を考えます:
これをそれぞれ自由度で割り、その比をとると…
この が従う分布を F分布(自由度 m, n) と呼びます。
確率密度関数
登場人物:
:自由度(分子・分母それぞれのカイ二乗分布の自由度)
- 分子
:1つ目のばらつき
- 分母
:2つ目のばらつき
:ベータ関数。分布の形を調整する役割(ガンマ関数と関係があり、
で表せる)
ちょっと難しいですが、もう少し詳しく説明すると、
- 自由度 m, n:比べるグループの大きさに関係する数字
- 分子 U/m, 分母 V/n:2つのバラつきを比べている(分散をそのまま比べると扱いづらいので、一度カイ二乗分布に変形し、自由度で割った形になっています。)
- ベータ関数 B:ガンマ関数を使って形を整える「分布の調味料」
※F分布の式は、ガンマ関数で書かれることもあれば、ベータ関数で書かれることもあります。どちらも同じ意味です。今回はベータ関数で書きました。ガンマ関数とベータ関数は親戚みたいな関数で、どちらを使っても同じ分布の形になります。
図式化すると、
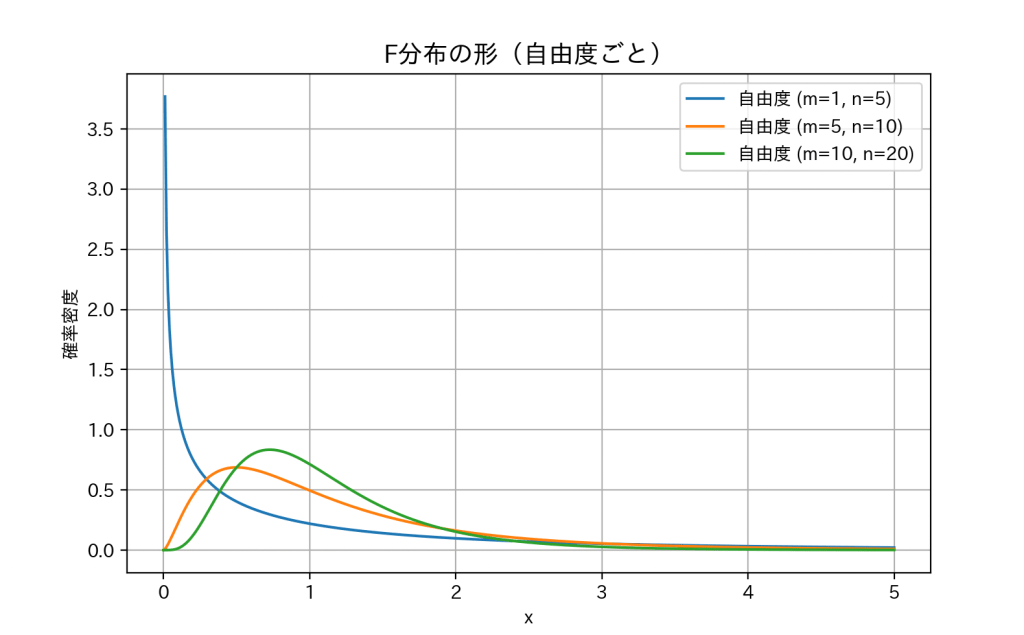
F分布は、カイ二乗分布を使って作られた分布です。そのため、形もカイ二乗分布と似ていて、左に山が寄って右に裾が長いのが特徴です。
ただし、分散の比を扱う分布なので、右に裾が長いです。
F分布の期待値(平均値)の式はこちらです。
は期待値です。
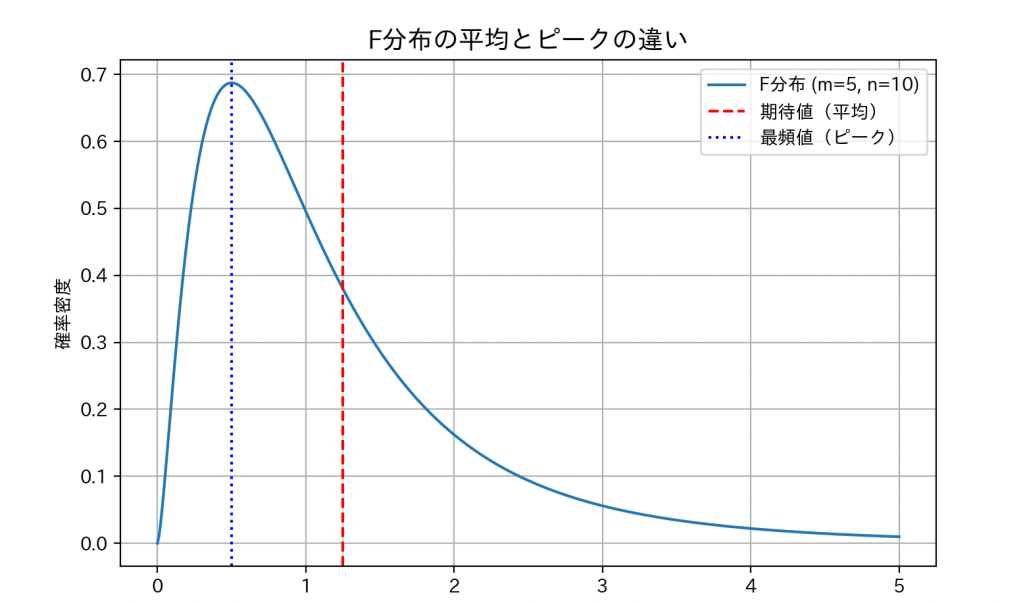
F分布の期待値は、自由度 nが大きくなるにつれて 1 に近づきます。
ただし、平均の位置とグラフの山のピーク(最もよく出る値)は必ずしも一致しません。
これは、F分布が右に長い裾を持っていて、平均が右に引っ張られるからです。