中学生でも分かる！？統計＆機械学習の数学〜微分・積分・最小二乗法・ロジスティック回帰・尤度最大化〜

ようこそ、恒例となってきました「中学生でもわかる！？統計（&機械学習）数学」シリーズへ。
今日のテーマは、

~~多くの人がつまづいたであろう~~「微分・積分」
微分を使って誤差を最小にする「最小二乗法」
Yes/Noを予測する「ロジスティック回帰」

です。
題名からして難しそうに聞こえるかもしれませんが、イメージできるようになれば怖くありません。

では、行ってみましょーーー！！！

電車旅でおさらいしよう、微分と積分

「微分？積分？？は？？？意味分からん！私これのせいで数学で挫折したんですけど！？」という方も少なくないでしょう。
私もそうです（おい）

そんなあなたのために、電車旅で例えてみましょう。

微分

電車は加速したり減速したりしますよね。
「今ちょうどこの瞬間、どれくらいの速さで走っている？」を調べるのが微分です。

イメージとしては、

東京駅を出発してすぐは：まだゆっくり
しばらく走ると：ものすごく速い
停車駅に近づくと：また減速

「坂道の傾き」みたいに、その瞬間の変化率を数字で表すのが微分なんです。
ボールを坂に置いたら転がっていく、その転がりやすさを測るイメージです。

式はこちら。

$\frac{dy}{dx}$

登場人物：

y：移動した距離（縦軸に相当）
x：時間（横軸に相当）
dy/dx：「時間の変化に対して、距離がどれだけ変わったか」＝瞬間の速さ

次に、微分を表すグラフを見てみます。

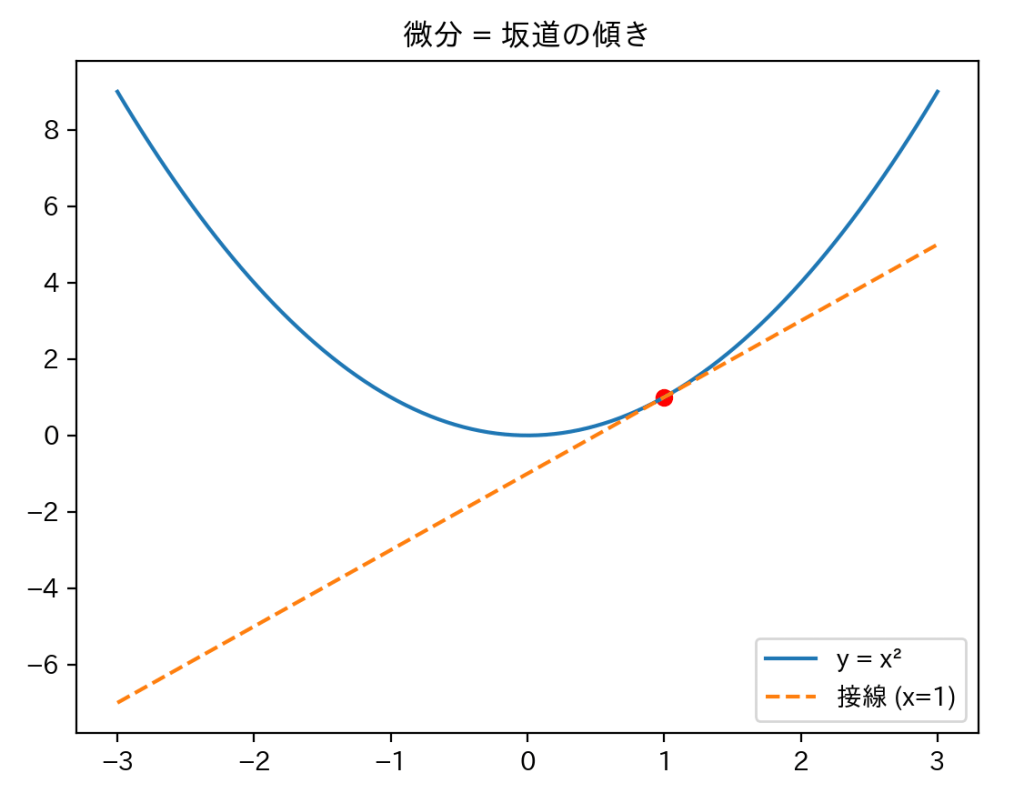
y=x² の x=1における微分は 接線の傾きです（f′(1)=2）。
（微分＝瞬間の変化率＝接線の傾き）

グラフのその点における瞬間の変化率で、接線の傾きに等しいです。

※「あれ、昔習った『lim（リミット＝極限）』が今回の式に出てこなかったぞ…」という方、鋭い！！その式も存在します。
でも今は接線の傾き＝微分とイメージできればOKです！

積分

今度は「東京から大阪まで、結局どれくらい走ったの？」を考えます。
区間ごとの移動を全部合計すると、総走行距離がわかります。
これが積分です。

$\int f(x) \, dx$

∫（インテグラル）：足し合わせる合図
f(x)：区間ごとのスピードや変化の大きさ
dx：小さな時間のかけら
∫ f(x) dx：「小さな区間での移動距離をぜんぶ足して、合計を求める」

イメージとしては「駅と駅の間の距離を少しずつ足していったら、東京〜大阪の総距離になる」ということです。

これの数式は基本形です。実際の使い方としては、

$\int_a^b f(x)\,dx$

a, b：x軸の区間（スタートとゴール）
意味としては「x=aからx=bまでの範囲で足し合わせる」

つまり「グラフとx軸に挟まれた範囲の面積（符号付き）」を表します。

積分も一度グラフで見てみましょう。

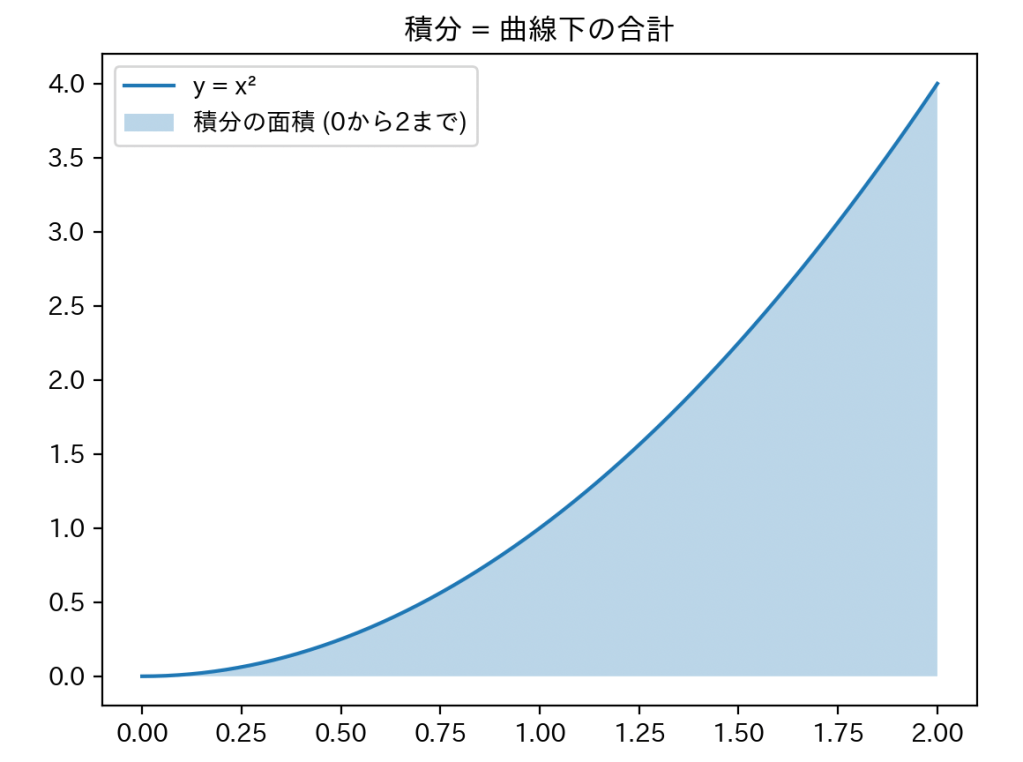
例えば y=x²のグラフで、0から2までの面積を積分するとこうなります：

$\int_0^2 x^2 \, dx = \tfrac{8}{3}$

ここでは敢えて途中式を書きませんが、
「積分すると面積が出せるんだ！」というイメージだけつかめば十分です。

微分・積分おさらい

微分：「今この瞬間の速さ」＝坂道の傾き
積分：「全部の距離を足した合計」＝曲線下の面積

微分は後ほどまた現れます。お楽しみに（？）

微分と最小二乗法

二乗誤差って何？

まずはこの表をご覧ください。

点と直線のズレ（赤線）を「誤差」と呼びます。
ズレを二乗して合計したものが「二乗誤差」です。

$E(\beta) = \sum (y - \hat{y})^2$

登場人物：

E(β)：誤差の大きさをまとめた式（「全体のズレ度」を表す）
y：実際のデータ（観測された値）
ŷ（yハット）：直線が予測した値
(y – ŷ)²：誤差を二乗してプラスにしたもの
Σ（シグマ）：それらを全部足す合図

微分で誤差を最小化する

この誤差をできるだけ小さくしたい。
そこで使うのが「微分」です。

先ほどの二乗誤差の数式を、微分の数式と組み合わせます。

$\frac{d}{d\beta} E(\beta) = 0$

d/dβ：βに関して「どっちに坂を下るか」を調べる操作
=0：坂の傾きが0になるところ＝谷底＝誤差が最小

これを解くと「最も実際のデータとズレが小さくなる直線の傾き・切片」が求まります。
これが「最小二乗法」。名前はかっこいいですが、やっているのは「一番フィットする直線探しゲーム」です。
イメージ図としてはこちら。

図の中では、候補2の線が一番点とのズレ（誤差）が少なそうですね。
これが最小二乗法の考え方です。

ロジスティック回帰

Yes・Noを予測したいときに便利なのがロジスティック回帰です。
過去の記事ではロジスティック回帰とはそもそも何か説明しているので、そちらも是非読んでみてくださいね。

そして、ロジスティック回帰の心臓部にあるのが「シグモイド関数」です。

$\sigma(z) = \frac{1}{1 + e^{-z}}$

σ(z)：シグモイド関数（答えは0〜1の間に収まる）
z：切片、係数、説明変数など、入力データをまとめて1つのスコアにしたもの
e：ネイピア数（約2.718…、グラフにS字を描くための根本的な材料）

グラフはS字カーブです。
下のグラフは回帰分析の記事でも紹介したものですが、もう一度見てみましょう。

z が大きければ σ(z) ≈ 1（Yes寄り）
z が小さければ σ(z) ≈ 0（No寄り）

ロジスティック回帰の曲線は、説明変数と結果の関係によって S字にも逆S字にもなります。
「歩数が多いとメタボが減る」なら右下がりの逆S字、「歩数が多いとリスクが増える」なら右上がりのS字になります。

尤度最大化

普通の回帰（最小二乗法）は「ズレを最小化」でした。
ロジスティック回帰は逆で、「正解を当てる確率（尤度）を最大化」します。

$L(\beta) = \prod p_i^{y_i} (1 - p_i)^{(1 - y_i)}$

L(β)：モデル全体の「当たりやすさ」
pᵢ：データ i が Yes になる確率（シグモイドの出力）
yᵢ：実際の答え（Yes=1, No=0）
Π（パイ）：全部掛ける 合図（Σの“掛け算版”）
$p_i^{\,y_i}\,(1-p_i)^{\,1-y_i}$ ：データ1つ分の当たり確率
→ これを 全部掛け合わせる と、全データの尤度になる

前に尤度の説明で、正規分布と指数分布では尤度関数を求める式の掛け算の中身が異なると説明しました。
ロジスティック回帰でもその考え方は共通しており、式の形は違いますが「データ1つ1つのもっともらしさを全部掛け算する」という流れは共通です。

図式化すると、以下の通りになります。

この赤い点線と対数尤度が交わる点が最尤推定値、つまり尤度最大化の結果なのです。

つまり、ロジスティック回帰での尤度最大化は、
「どんな傾きや切片なら、このデータのYes/Noを一番もっともらしく説明できるか？」を探す作業です。
これによって、最もデータに合った回帰係数（β）を求めることができ、予測モデルとして使えるようになります。
保健師の現場では、リスクの高い人を早めに見つけて指導につなげたり、集団全体の傾向を把握したりするのに役立ちます。

まとめ

以上、微分を利用した最小二乗法、ロジスティック回帰に登場する数学についてゆるっと解説してきました。

まとめると、

微分：坂道を転がるボールが谷底で止まる場所を探す。
積分：グラフの中の範囲で作られた図形の面積を求める。
最小二乗法：ズレをできるだけ小さくする直線探し。
ロジスティック回帰：Yes/Noを予測する。
シグモイド関数：Yes/NoをなめらかにつなぐS字カーブを作る。
尤度最大化：当たり（尤度）をできるだけ増やす方法。

難しい数式に見えても、概要さえおさえれば何となく統計や機械学習の仕組みがわかるようになってきます。

次回もまた、お会いできるのを楽しみにしています。
では、さらばだ！

落ちこぼれナースの統計チャレンジ

中学生でも分かる！？統計＆機械学習の数学〜微分・積分・最小二乗法・ロジスティック回帰・尤度最大化〜