はいさい。「中学生でも分かる！？機械学習の数学」コーナーの時間です。

今回のテーマはこちら！！！
エントロピー・ジニ不純度・情報利得・アンサンブル学習！

…はい、皆さん、いつも通り頭にハテナマークがついていますね。
いつも通り、ゆるーく解説していくのでリラックスして読んでくださいね。

では、レッツゴー！！！

※今回の記事は、決定木・ランダムフォレストと関係があります。まだそちらの記事を読んでいない方は、そちらもご参照ください。

---

情報理論：エントロピー

エントロピーとは「データがどれくらいごちゃごちゃ（不確実）か」を表す数値です。

登場人物：

• H(p)：エントロピー（データの混ざり具合）
• ∑：総和（足し算の記号、「全部足してください」の意味）
• k：クラス（グループ）の数
• p_i：クラス iに属する確率
• log⁡₂：2を底にした対数（情報を「ビット」で数えるため）
• 先頭の「-」：確率の対数が負の数になるため、それを正の数に変換する役割

つまり、結果が大きいほどデータが「ごちゃごちゃ」、小さいほど「スッキリ」です。

ジニ不純度

ジニ不純度も「ごちゃごちゃ度」を測る別の方法です。計算は少しシンプル。

登場人物：

• G(p)：ジニ不純度
• p_i²：そのクラスに属する確率を二乗
• ∑：それらを全部足す
• 1− ：「1から引く」ことで、ごちゃごちゃ度を表す

つまり、 0なら「完全にスッキリ」、0.5前後なら「半分半分で混ざってる」状態です。

先ほど出てきたエントロピーと図で比較してみましょう。
（※クラスを2つに分ける前提。エントロピーの底は機械学習でよく用いられる2とします）

エントロピーは1.0に近いほど、ジニ不純度は0.5に近いほど不確実度が高い状態を示しています。

情報利得

決定木が「どこで分けるか？」を決めるために使う基準です。

登場人物：

• IG：情報利得（分けて得した量）
• H(親)：分ける前のエントロピー（混ざり具合）
• H(子_j)：分けた後の各グループのエントロピー
• N_j：グループ jに入ったデータ数
• N：全データ数
• ：グループ jの割合（重み）

「分ける前の混ざり度」－「分けた後の混ざり度（人数比で平均）」＝情報利得。
数値が大きいほど「良い分け方」です。

今回はエントロピーを例に出しましたが、ジニ不純度を使って計算することもできます。HがGになるだけです。

では、情報利得の考え方を図にしてみます。

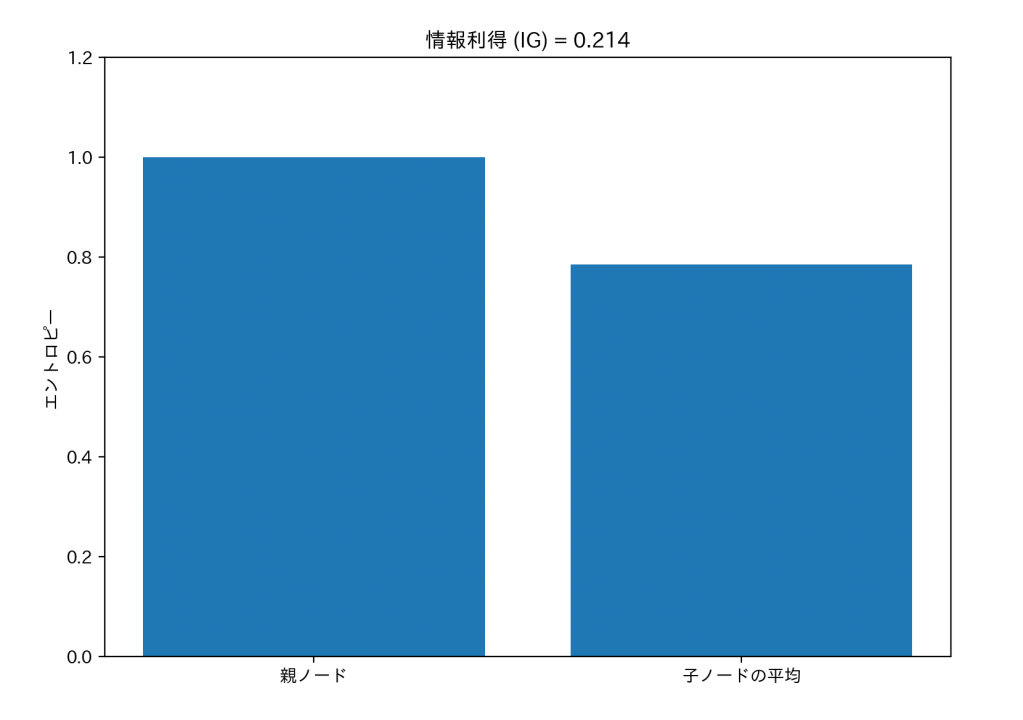
左の棒は親ノードのごちゃごちゃ度（エントロピー）、右の棒は分けたあと（子ノード）の平均ごちゃごちゃ度を示しています。
この例では、親の方が数値が高く、子ノードで少し下がっていますね。この差が情報利得（IG=0.214）です。
分けることで不確実さが減り、少し整理されたことが分かります。
情報利得が高いほど、「うまく分けられた！！」ということになります。

エントロピー・ジニ不純度・情報利得は、決定木やランダムフォレストで「どの分け方が一番いいんだろう？」と決めるのに役立ちます。

アンサンブル学習の考え方

決定木・ランダムフォレストの記事でも説明した通り、「一人の決定木」だと極端すぎたり、偏った判断をすることがあります。
そこで登場するのが アンサンブル学習です。

その代表が「バギング（Bagging）」＋「多数決」です。

1. データをランダムに分けて、何本もの決定木を育てる（バギング＝Bootstrap Aggregating）。
2. 各木が「この人はAクラスだ！」「いやいやBクラスっしょ」「Aクラスに違いないでごわす」と判定する。
3. 最後は「多数決」で決定！

これがランダムフォレストの基本原理です。

まとめ

• エントロピー・ジニ：混ざり具合を測る数式
• 情報利得：分けてどれだけスッキリしたかを数値化
• アンサンブル学習：多数決で安定した予測

いつものように、難しい数式でも、パーツごとに見れば「なるほど！」と分かりやすくなります。

焦らず、ゆっくりと学んでいきましょう。

では、次の記事でお会いしましょう！！！