中学生でも分かる！？統計&機械学習の数学〜欠損値処理と特徴量エンジニアリング編〜

前回の記事では、欠損値処理と特徴量エンジニアリングの理論について紹介しました。
まだ見ていない方はそちらもご参照くださいね。

今回はその続きを「数式」として見ていきます。
でも大丈夫！！いつもより難易度はかなり低いですから！！！本当ですよ！！！
（~~ただし最後の部分を除く~~）

早速始めちゃいましょう。レッツゴーーーーーー！！！！

平均値

「んなもん知っとるわ！！！わし小学生ちゃうわ！！！アホか！！！」という方も、一旦おさらいしておきましょう。

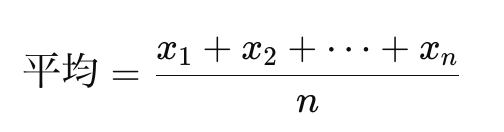
患者さん10人の体温を足して10で割る、といういつもの計算ですね。
前回お伝えした平均値補完は、欠損値がある時にこの「平均」で空欄を埋めてしまう方法です。

ただし、これは外れ値に弱いというデメリットがあります。

例えば、体温の平均を求めるとすると、36.5度の人がほとんどだったとしても、集団の中に40度とか34度の人がいたら、平均値がそちらに引っ張られてしまうのです。

「あれ？？うちの病棟、もしかしてみんな高体温（低体温）！？」と誤解する恐れがあります。

中央値

中央値は順番に並べて真ん中を取ったものです。
例えば9人の体温を並べると、5番目の値が中央値です。

偶数人、例えば10人の場合は5番目と6番目の人の平均値です。

中央値補完は、欠損が出たら「みんなの真ん中っぽい値」を入れるイメージです。

最頻値

最頻値は 一番多く出てくる値です。
例えば「体温が36.5度の人が一番多い」なら、36.5度が最頻値です。

ただし、最頻値が複数になることもあります。
例えば、36.4度の人と36.7度の人が同数になることもあります。
この場合は「どれを採用するか」決めなければなりません。

Zスコア標準化

データの「平均との差」を「ばらつき（標準偏差）」で割ったものです。

$Z = \frac{X - \mu}{\sigma}$

$X$ ：個人の値
$\mu$ ：平均値
$\sigma$ ：標準偏差

例えば、「あなたの身長が平均よりどれくらい高いか」を偏差値風に表す方法です。

min-max 正規化

データを 0〜1の範囲に変換する式です。

$X' = \frac{X - X_{\min}}{X_{\max} - X_{\min}}$

登場人物：

$X$ ：いま注目している人のデータ（例：ある患者さんの体温）
$X_{\min}$ ：その項目の最小値（例：集団で一番低い体温）
$X_{\max}$ ：その項目の最大値（例：集団で一番高い体温）
$X - X_{\min}$ ：最小値からの距離（例：特定の患者さんの体温が「一番低い人よりどれくらい高いか」）
$X_{\max} - X_{\min}$ ：全体の幅（例：最高体温と最低体温の差）

体温が35.0〜40.0℃の範囲なら、36.5℃は「0.3」くらいの位置に変換されます。
まるで「クラスで背の順に並んで、0（いちばん低い人）〜1（いちばん高い人）」に換算する感じです。

回帰補完の数式

実は、これは過去に登場しています。回帰分析の数学記事をご参照ください。
今までの数式より大幅に複雑ですが、こちらもパーツごとに説明しているので諦めずに読んでみてください。

~~難易度の温度差で風邪をひかないでくださいね。~~

多重代入法の数式

多重代入法は、大きく分けて補完、分析、統合の段階を踏みます。
このうち最後の統合の部分をきちんと数式で定めたのが、 Rubinのルール です。

補完（Imputation）

欠損データを含む元データ $D$ から、補完済みデータセットを $m$ 個作成します。

$D_1, D_2, \ldots, D_m$

登場人物：

$D$ ：元のデータセット（欠損あり）
$D_i$ ：補完後のデータセット（i = 1,2,…,m）
$m$ ：補完したデータセットの数（例えば5個や10個）

「空欄をランダムに埋めた複数バージョンのデータ」 を用意する段階です。

分析（Analysis）

各データセット $D_i$ に対して統計モデルを推定します。
推定値と分散を下記のようにして得ます。

$\hat{\theta}_i, \quad U_i \quad (i = 1, \ldots, m)$

登場人物：

$\hat{\theta}_i$ ：i番目のデータセットで得られた推定値（例：回帰係数、平均値）
$U_i$ ：その推定値の分散（推定の不確実性の大きさ）
$i$ ：補完データセットの番号

「補完パターンごとに結果が少しずつ違う」のがポイントです。

統合（Pooling）

推定値の統合

すべての結果をまとめ、最終的な推定値 $\bar{\theta}$ を計算します。

$\bar{\theta} = \frac{1}{m} \sum_{i=1}^m \hat{\theta}_i$

登場人物：

$\bar{\theta}$ ：最終的な推定値（統合結果）
$m$ ：補完データの数
$\hat{\theta}_i$ ：i番目の補完データからの推定値
$\sum$ ：全部を足して平均を取る記号

「全部の結果を平均して代表値を出す」というのがポイントです。

分散の統合

分散は「各データセットの平均分散 + 推定値間のばらつき」で表されます。

$T = \bar{U} + \left(1 + \frac{1}{m}\right) B$

登場人物：

$T$ ：最終的な分散（全体の不確実性）
$\bar{U}$ （within-imputation variance）
$U_i$ ：各データセットの分散（「そのデータの中の不確実性」）
$\bar{U} = \frac{1}{m} \sum_{i=1}^m U_i$ ：すべてのデータセットの分散の平均
→補完ごとの「内部のばらつき」の平均値
$B$ （between-imputation variance）
$\hat{\theta}_i$ ：各データセットの推定値
$\bar{\theta}$ ：推定値の平均
$B = \frac{1}{m-1} \sum_{i=1}^m (\hat{\theta}_i - \bar{\theta})^2$
→補完データ間でのばらつき（「補完ごとに結果が違う分の不確実性」）
$(1 + 1/m)$
$m$ ：補完データセットの数
$(1 + 1/m)$ ：調整係（補完データが少ないときの誤差を見込んで“ちょっと上乗せ”する係数）

おわりに

今回の数学記事はいかがだったでしょうか？

前半と後半の難易度の差が激しすぎましたね。

でも結局は基本的な数学の延長のようなものなので、これからも肩の力を抜きながら読んでくださいね！

では、次の記事でお会いしましょう！！！

落ちこぼれナースの統計チャレンジ

中学生でも分かる！？統計&機械学習の数学〜欠損値処理と特徴量エンジニアリング編〜

平均値

中央値

最頻値

Zスコア標準化

min-max 正規化

回帰補完の数式