今回のテーマは「モデルの性能」と「汎化性能（generalization）」です。

突然ですが、「なんでも完璧にこなす新人看護師」がいたら、ちょっと怖くありませんか？
最初の1ヶ月で患者対応も記録も完璧。失敗ゼロ。
……え？　むしろ安心？？

でも、現場の先輩は「今はうちの病棟でうまくいってるけど、別の病棟に行って応用がきかなくなったらどうするんだろう…？」と思うかもしれません。

実はこれ、機械学習モデルにも当てはまる話なんです。

今回は、「このモデルは完璧すぎないかな？？本当に応用が効くのかな？？」と評価するために必要な、機械学習の考え方について紹介します。

それでは、レッツゴーーーー！！！

---

過学習：訓練データばかり見すぎ！！

モデルが「訓練データ」で勉強するとき、まるで国家試験の過去問をひたすら暗記しているような状態になります。
それ自体は悪くないのですが……

• 過去問の数字を全部覚える
• 解答パターンだけを完璧に再現
• 新しい問題に出会うと「何これ？？？進○ゼミでこんな問題出なかったけど？」

これがまさに過学習（overfitting）です。

現場で言えば、
「いつも同じ患者さんだけ見てると、新しい症状に対応できなくなる」状態ですね。

つまり、訓練データで高得点＝臨床で使えるとは限らないんです。
モデルでも、同じ考え方をします。

過学習のイメージ図としてはこちらです。

黒い点が実際に測ったデータです。

それに沿ったモデルを作るのが目的なのですが、

青の線は点をうまく捉えられていない。
一方、緑の線は、ノイズに捉われて、歪な形になってしまっています。これが過学習なのです。

点を捉えられていて、かつシンプルな形のオレンジの線が、応用が効きやすいモデルなのです。

バイアス・バリアンスのトレードオフ

さて、次に出てくるのが難しそうな言葉であるバイアスとバリアンスです。でも怖がらないでください。

• バイアス（bias）：「思い込みの強さ」
  例：データをざっくり見すぎて「全員健康そう！！」と決めつける
• バリアンス（variance）：「気分のブレ」
  例：少しの違いで診断がコロコロ変わる

理想のナースは「観察も的確で、ブレない人」。
でも、思い込みゼロでブレもゼロなんて人間、いませんよね。
モデルも同じで、「シンプルすぎず、複雑すぎず」のバランスが大事。

このバランスを取ることを「バイアス・バリアンスのトレードオフ」と呼びます。

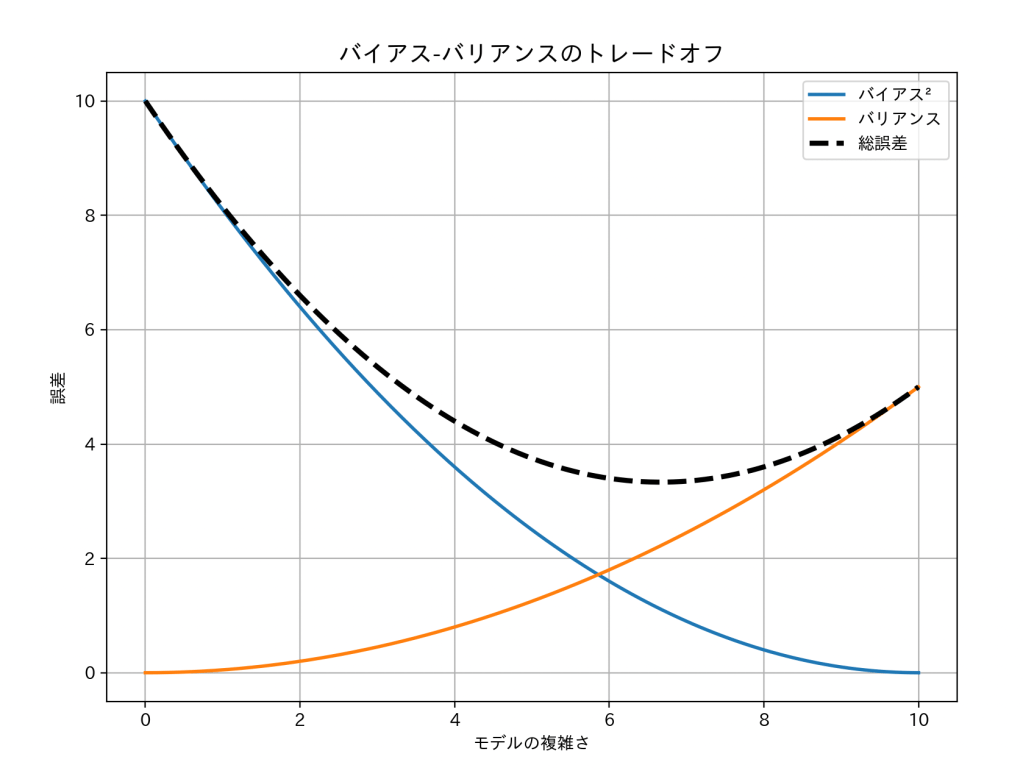
図にすると、バイアスが低くなるほど、バリアンスが高くなっています。
（バイアスが二乗なのは、ズレの大きさを見るためにプラスの値もマイナスの値も二乗しているからです）

モデルの複雑さが6付近になると、総誤差が低くなります。
これが、「ざっくりしすぎず、応用にも対応できる」モデルなのです。

6より左は「学習不足」、6より右は「過学習」の傾向にあります。

交差検証（k-fold CV）：現場力を試す！

さて、どうすれば「本番に強い」モデルを作れるのでしょうか？
答えは割とシンプルで、練習のやり方を工夫することです。

「k-fold 交差検証」というのは、
モデルを何度もテストして現場力を試す方法です。

たとえば、あなたが新人看護師の指導者だとして、
1人の看護師を「A病棟」「B病棟」「C病棟」に順番に配属してみる。
どこでも安定して動けたら、看護師としての実力は本物です。

同じように、データを何分割もして「どのデータでもうまく予測できるか」を確かめるのが交差検証です。
偶然うまくいっただけじゃないか？を見抜くためのテストです。

イメージ図はこちら。

各行（Fold）とは1回の検証です。

青が「テストデータ」（実際にモデルの性能を試す相手）、灰色が「訓練データ」（学習するためのデータ）です。

このように、k-fold交差検証では、全部のデータが一度はテストに使われています。

正則化（L1・L2）：余計なこだわりを手放す

さて、最後に正則化（regularization）です。
これは一言で言うと、「頑張りすぎるモデルに、ちょっとブレーキをかける仕組み」です。

L1正則化とL2正則化という2種類がありますが、
直感的にはこう考えると分かりやすいです。

• L1正則化： いらない特徴量をスパッと切る。
  → 「それ、本当に必要？」と問う冷静な先輩看護師。
• L2正則化： すべての特徴量をほどよく抑える。
  → 「まあまあ、全部ほどほどにね」と言う優しい先輩看護師。

つまり、どちらも「やりすぎ防止」ですが、
L1は不要な要素をゼロに、L2は全体を控えめにするタイプです。

現場でも、「情報を全部抱え込むより、本当に大事なポイントに絞る」方がミスは減りますよね。
それと同じ理屈です。

これも一度図にしてみます。

ペナルティ（罰則項）とは、モデルの暴走を防ぐためのものです。やり過ぎ防止、という意味で覚えておきましょう。

ところで、L1のグラフは0に尖った角があるのに、L2は滑らかですね。

L1はスパッと判断して、L2はほどよく抑えるという特徴がグラフに出ています。

ちなみに、L1を使ったものをラッソ回帰（Lasso）、L2を使ったものをリッジ回帰（Ridge）、L1とL2のバランス型をエラスティックネット（Elastic net）と言います。

こちらも図にしてみました。

この図の丸い青線がリッジ回帰、紫色の四角形がラッソ回帰、他の色は全てエラスティックネットです。

このように、柔軟にモデルをコントロールしていきますよ、という考え方です。

---

まとめ

今日のまとめです。

• 過学習：訓練に特化しすぎ
• バイアス：思い込みが強い
• バリアンス：ブレが大きい
• 交差検証：訓練の見直し法
• 正則化：やりすぎ防止策

看護師さんだって、応用力が効く人が重宝されますよね。
モデルも同じで、どんな現場でも安定して力を発揮できる人が最強です！