落ちこぼれナースの統計チャレンジ

元落ちこぼれ看護師（保健師）が、私と同じく統計にドキドキしている看護学生や保健師さんに、簡単な言葉で届けるために始めたブログです。

中学生でも分かる！？機械学習の数学〜バイアス・バリアンス・正則化〜

今回は「モデルの性能と汎化性能ってどうやって数式で考えるの？」というお話です。

モデルの性能と汎化性能については前回の記事に詳しく載っているため、こちらが未読の方は先にお読みください。

お馴染みの「中学生でも分かる！？」シリーズで、今回もやさしく学びましょう！

それでは、レッツゴーーーー！！！

誤差を分解してみよう

モデルの誤差を示す式は、下記の通りです。

\text{MSE} = \text{Bias}^2 + \text{Variance} + \text{Irreducible Error}

登場人物：

  • \text{Bias}^2：バイアス２（思い込みの強さ）
  • \text{Variance}：バリアンス
  • \text{Irreducible Error}：不可避誤差（ノイズ）

このバイアス、バリアンス、不可避誤差のバランスが「モデルの汎化性能」を決めます。
バイアスを下げようと頑張りすぎると、バリアンスが上がってしまう。
これが バイアス・バリアンスのトレードオフ です。

数式で見える「過学習」

「学習しすぎて失敗」＝過学習です。
これは数式でいうと、バリアンスが大きすぎる状態です。

  • 学習データ：完璧に当てはまる
  • 新しいデータ：全然当たらない
\text{Loss} = \sum_i (y_i - \hat{y}_i)^2

登場人物：

  • text{loss}：損失関数
  • y_i：実際の値（真の答え）
  • \hat{y}_i：モデルの予測値
  • (y_i - \hat{y}_i)^2：誤差の二乗（ズレの大きさ）
  • \sum_i：全データの誤差を合計

この数値が大きいと、学習しすぎて新しいデータに対応できていない可能性が高いです。

これを最小化するのが「最小二乗法」や「回帰分析」です。

バイアス²＋バリアンスのバランスを見る

\text{Error} = \text{Bias}^2 + \text{Variance}

モデルの複雑さを上げていくと：

  • バイアス² ： 減る
  • バリアンス ： 増える

その合計（総誤差）が一番小さくなる地点が、
最適な複雑さ＝汎化性能が最高の点です。

前回の記事の図をもう一度見てみましょう。

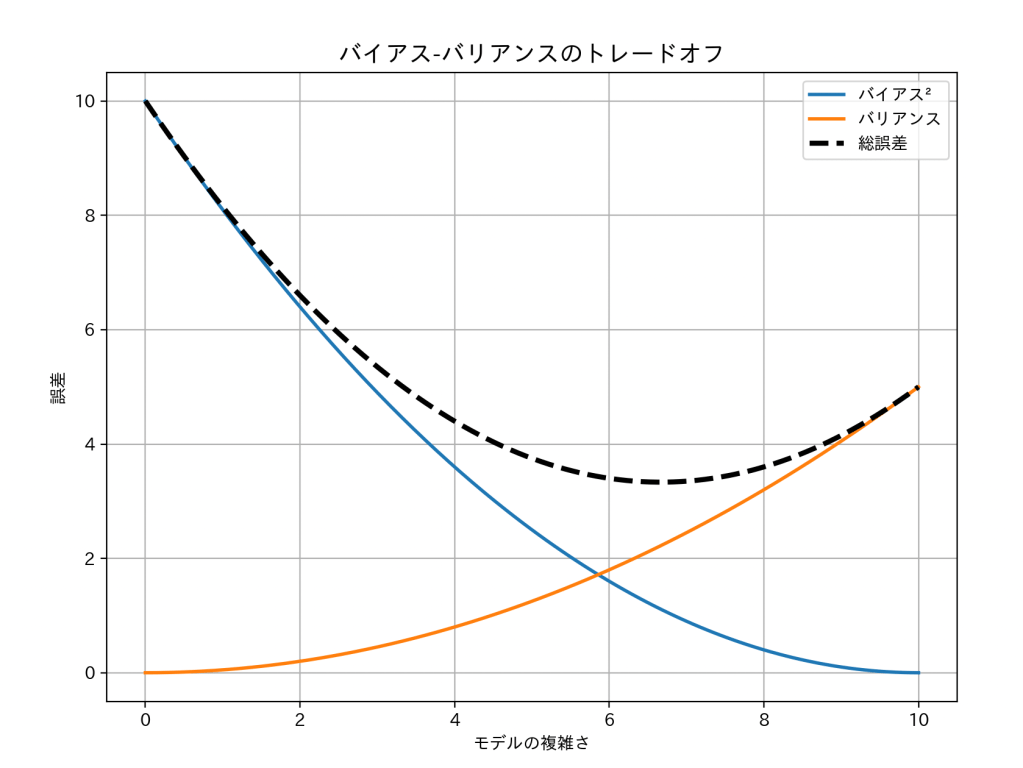
この図だと、複雑さ6あたりがまさにそれですね。

正則化とペナルティ（罰則）

ここで登場するのが 正則化（regularization）です。
これは「やりすぎモデルにペナルティ（罰）を与える」という仕組みです。

\text{Loss}_{\text{reg}} = \sum_i (y_i - \hat{y}_i)^2 + \lambda \times \text{Penalty}

登場人物：

  • \sum_i (y_i - \hat{y}_i)^2：通常の誤差（二乗誤差）
  • λ ：罰則の強さ（大きいほど制約が強い）
  • {Penalty}：正則化項（L1、L2など）

L1正則化（ラッソ回帰）

\text{Loss}_{\text{Lasso}}=\sum_i (y_i-\hat{y}_i)^2+\lambda \sum_j \lvert w_j\rvert

登場人物：

  • \sum_i (y_i-\hat{y}_i)^2：通常の二乗誤差
  • \lambda：罰則の強さ
  • \sum_j \lvert w_j\rvert：L1ペナルティ
  • w_j：係数（重み）

つまり、係数（重み）の絶対値の和をペナルティにしています。

L2正則化（リッジ回帰）

\text{Loss}_{\text{Ridge}} = \sum_i (y_i - \hat{y}_i)^2 + \lambda \sum_j w_j^2

登場人物：

  • w_j：各特徴量の重み（係数）
  • \sum_j w_j^2：L2ペナルティ（なめらかに縮める）

これで、モデルをなめらかにするのです。

L1＋L2の折衷（エラスティックネット）

\text{Loss}_{\text{ElasticNet}} = \sum_i (y_i - \hat{y}_i)^2 + \lambda_1 \sum_j |w_j| + \lambda_2 \sum_j w_j^2

登場人物：

  • λ1：L1ペナルティの強さ
  • λ2：L2ペナルティの強さ

このように、2つのペナルティを組み合わせて、より良いモデルにするため調整します。

まとめ

簡単にまとめると、

  • バイアス2：思い込みの強さ
  • バリアンス：ブレの大きさ
  • ペナルティ：モデルのやりすぎ防止
  • λ：ペナルティの強さ

数学はモデルを縛るためではなく、自由にさせすぎて失敗させないための優しさです。

何もかもバランスが大事ですね。

ではでは、次の記事でお会いしましょう！！！

ツシマ

, , ,

コメントを残す