落ちこぼれナースの統計チャレンジ

元落ちこぼれ看護師（保健師）が、私と同じく統計にドキドキしている看護学生や保健師さんに、簡単な言葉で届けるために始めたブログです。

中学生でも分かる！？機械学習の数学〜SVM・勾配ブースティングの数式〜

お待たせしました、毎回恒例の中学生でも分かる！？機械学習の数学シリーズです。

今回のテーマはSVM、勾配ブースティングの数式です。
そもそもSVM、勾配ブースティングって何？という方は過去記事をご参照ください。

今回も数式をやさしく分解して説明するので、ついて来てくださいね〜〜〜

それでは、レッツゴーーーー！！！！！！

SVMの数式

基本形

w \cdot x + b = 0

登場人物：

  • w：線の向きを決めるベクトル
  • x：データ
  • b：線の位置をずらす定数

この1本の線（または面）で、チームを分けるのが目的です。

ここで出てくる「・」とは、ベクトルの内積、いわゆる「wとxの向きや大きさを掛け合わせる特別な掛け算」です。

マージン最大化

SVMが特別なのは、できるだけ広い余白（マージン）をとることでした。
これを式で書くとこうなります。

\text{maximize } \frac{2}{|| w ||}

|| w ||の両側にある二本線は、ノルム（norm） と呼ばれるものです。簡単に言うと、ベクトルw の長さや大きさを表しています。

線の傾きを表すwが小さいほどマージンが広くなります。
「境界線がゆったり構えている」イメージです。

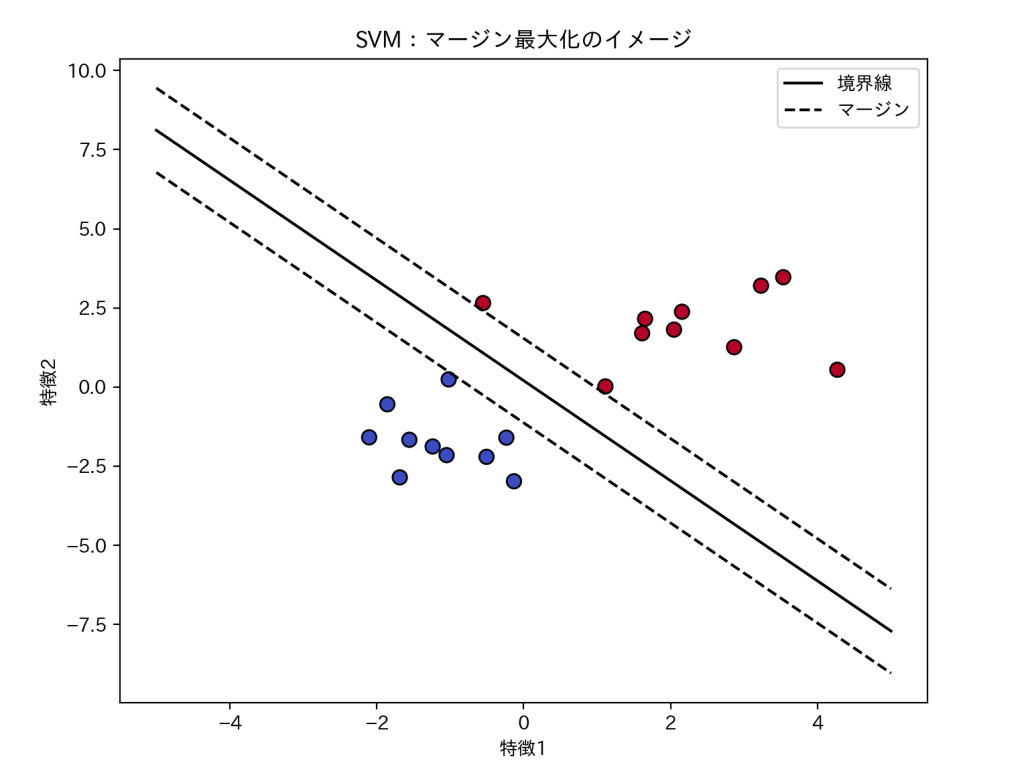
図にするとイメージしやすいですね。

間違えたくない！でも現実のデータでは上手くいかん…

現実のデータでは、厳密にデータを分けようとすると、うまくきれいに分けられないこともあります。
そのため、少しの誤差を許す「ソフトマージンSVM」という形にします。

\text{minimize } \frac{1}{2} || w ||^2 + C \sum_i \xi_i

登場人物：

  • C：厳しさを決めるパラメータ（大きいと厳しく、小さいと寛容）
  • \xi_i：各データがどれだけ間違えているか（スラック変数）
  • \sum_i \xi_i：各データの間違いを足していく

つまり、「できるだけ厳密に分けたいけど、多少の例外はOK」という現実的な折衷案です。

カーネル法

線では分けられない時は、空間でデータをとらえます。

K(x_i, x_j) = \phi(x_i) \cdot \phi(x_j)

登場人物：

  • \phi(x)：データの見方を変える関数
  • K：カーネル関数（距離の測り方）

代表例としては、

  • 線形カーネル（Linear Kernel）：シンプルで速い
  • RBFカーネル（Gaussian Kernel）：曲線で分けられる

があります。

勾配ブースティングの数式

予測を少しずつ改善する

ブースティングの考え方は「前回のミスを次で修正」です。

F_m(x) = F_{m-1}(x) + \eta h_m(x)

登場人物：

  • F_m(x)：m回目（今回）の予測モデル
  • F_{m-1}(x)：m-1回目（前回）の予測モデル
  • h_m(x)：新しく学んだ弱学習器
  • \eta：学習率（どのくらい修正するか）

つまり、「前回の予測＋今回のちょっとした修正」を何度も積み重ねて、少しずつ賢くなっていくのです。

イメージ図をご覧ください。

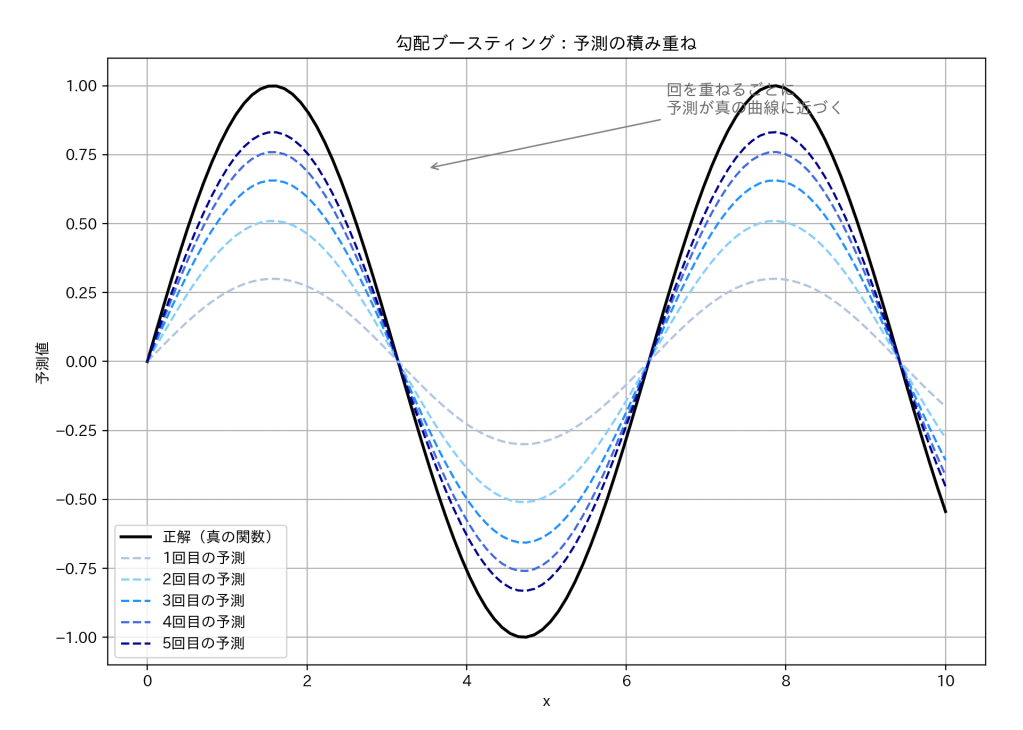
このように何度も予測を繰り返すことで、予測が正解に近づいていきます。

勾配って何？

「勾配」はどの方向に間違っているかを教えてくれるベクトルです。
数学的には誤差関数の傾きです。

g_i = - \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}

登場人物：

  • L(y_i, F(x_i))：損失関数（どれくらい間違えているか）
  • \partial：偏微分（他の要因はそのままにして、1つの変数だけ動かしたときの変化量）
  • g_i：そのデータに対して「どっちに直せばいいか」の方向

マイナス（−）がついているのは、「間違いを減らす方向に進む」、という意味です。

ブースティングではこのg_iを参考に、
「次はどこを直せばいいか」を決めていきます。

損失関数についてのグラフを見てみましょう。

分かりやすくするために、ここでは代表的な損失関数である「平方誤差損失関数」を例に説明します。
これは、予測値 F が正解 y から離れるほど損失が急激に大きくなる、放物線の形をしています。

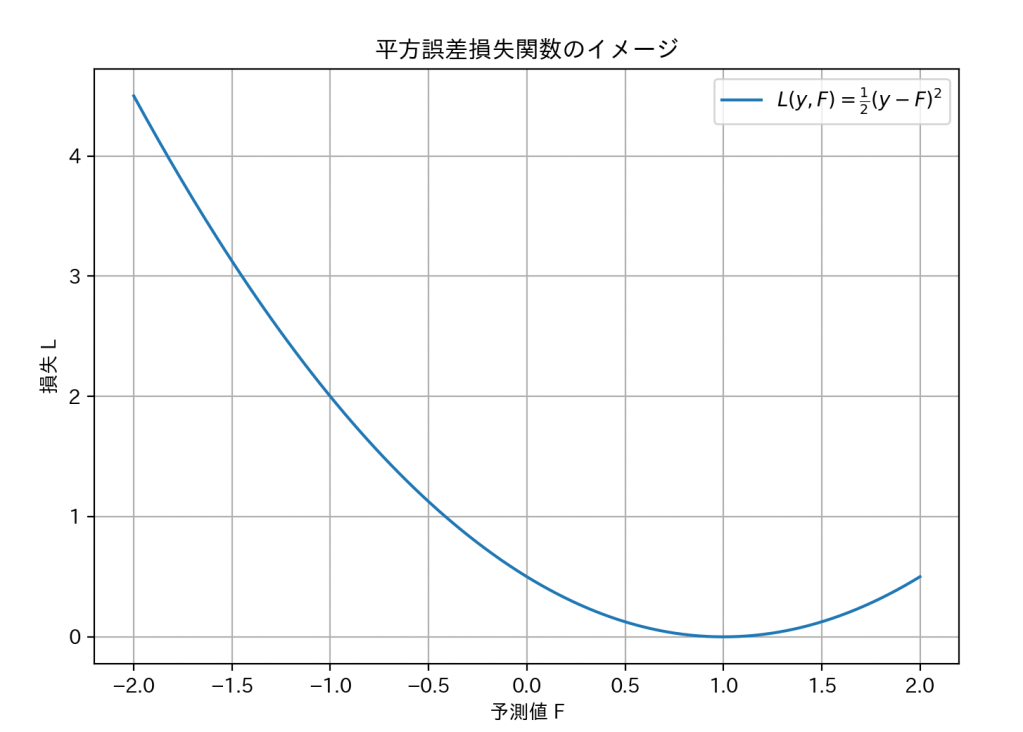
グラフの一番低い部分（このグラフでは1.0付近）が「損失（誤差）が最も小さい＝予測が一番正確な状態」です。
機械学習は、この谷底を目指してパラメータを少しずつ調整していくのです。

最後の予測

すべての弱学習器を足し合わせて最終予測を作ります。

F(x) = \sum_{m=1}^{M} \eta h_m(x)

登場人物：

  • M：全体のステップ数（弱学習器の数）
  • \eta h_m(x)：それぞれの小さな修正（微調整）

M回分の努力の積み重ねで、立派なモデルが完成しました。チャンチャン。

おわりに

今回の数学記事で理解を深められたでしょうか？

数学は見た目は難しいですが、少しだけでも親しみを持ってもらえると嬉しいです。

それでは、次の記事でお会いしましょう！！！

ツシマ

, , ,

コメントを残す