早速ですが、今回は回帰分析についてご紹介します！！

準備はよろしいでしょうか？？

いいともーーーーー！！！！

---

そもそも回帰分析って何ぞや

「回帰分析」と聞くと、なんだか数式だらけで難しそうに見えるかもしれません。
でもイメージとしてはとてもシンプルで、「ある要因が結果にどのくらい関係しているか」を調べる方法です。

例えば、

• 身長が高いほど体重も増える？
• 歩数が増えるほどメタボのリスクは減る？

こうした関係を数字で表せるのが回帰分析のすごいところです。

そしてここで衝撃の事実をお伝えします。
この回帰分析、実は「機械学習」の一種としても使われています。
統計の授業で出てきたあの回帰直線やS字カーブ、AIの世界でも立派に活躍しているんです。

ここでは、

• 線形回帰（単回帰分析、重回帰分析）
• ロジスティック回帰

を説明していきます。

線形回帰（Linear Regression）

線形回帰は、結果が数値の時に使い、直線を引いて「片方が増えると片方が増える／減る」関係をつかむツールです。

さらに、線形回帰は、「説明変数が1つだけか」「複数あるか」で呼び方が異なります。

単回帰分析

要因が1つだけのときに使います。

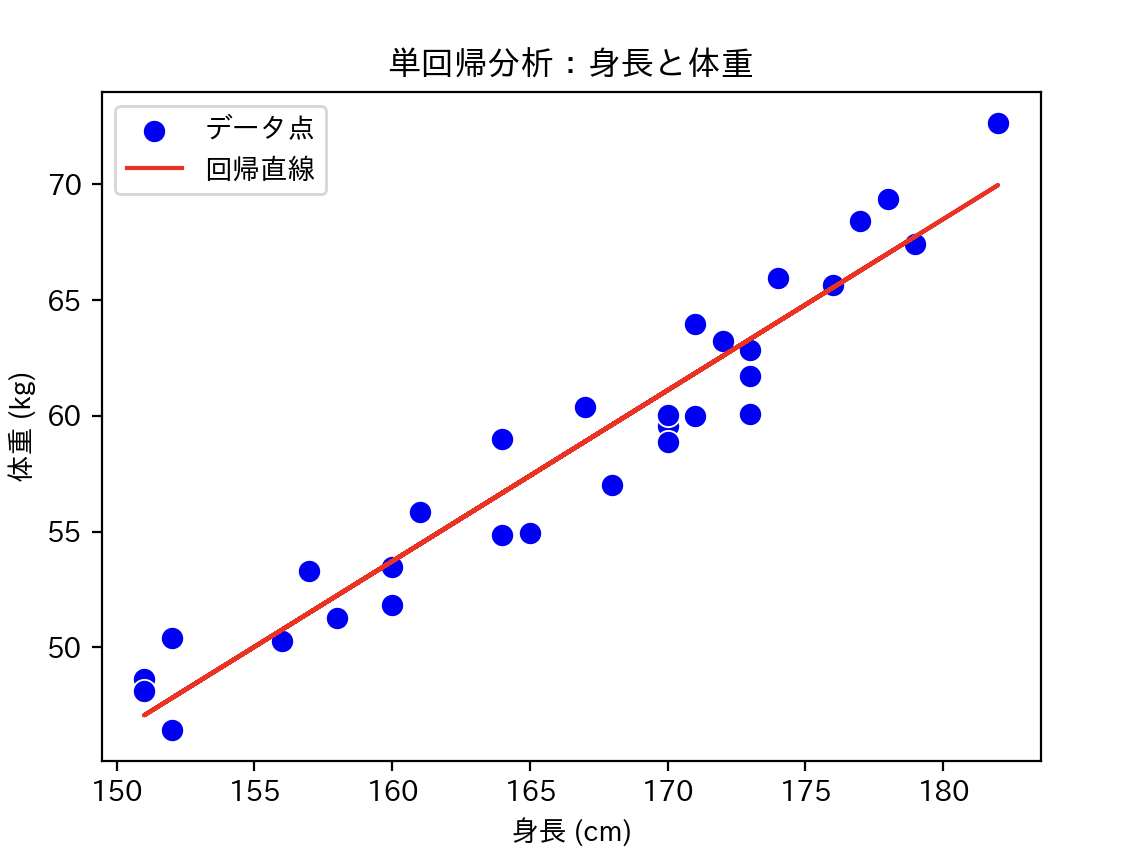
例：身長と体重

• 横軸：身長(cm)
• 縦軸：体重（kg）

仮に結果が「身長が1cm高いと体重が0.7kg増える」なら、それが単回帰分析の成果です。

数式についてはこちらの記事で解説しています。
よろしければご覧ください。

重回帰分析

要因が2つ以上あるときに使います。

例：

• BMI
• 収縮期血圧(mmHg)
• 空腹時血糖(mg/dL)

これらをまとめて体重変化にどう影響するかを分析します。
どの要因がどれくらい効いているかを一度に確認できるのがポイントです。

ちょっと分かりにくくなったので、図にしてみました。

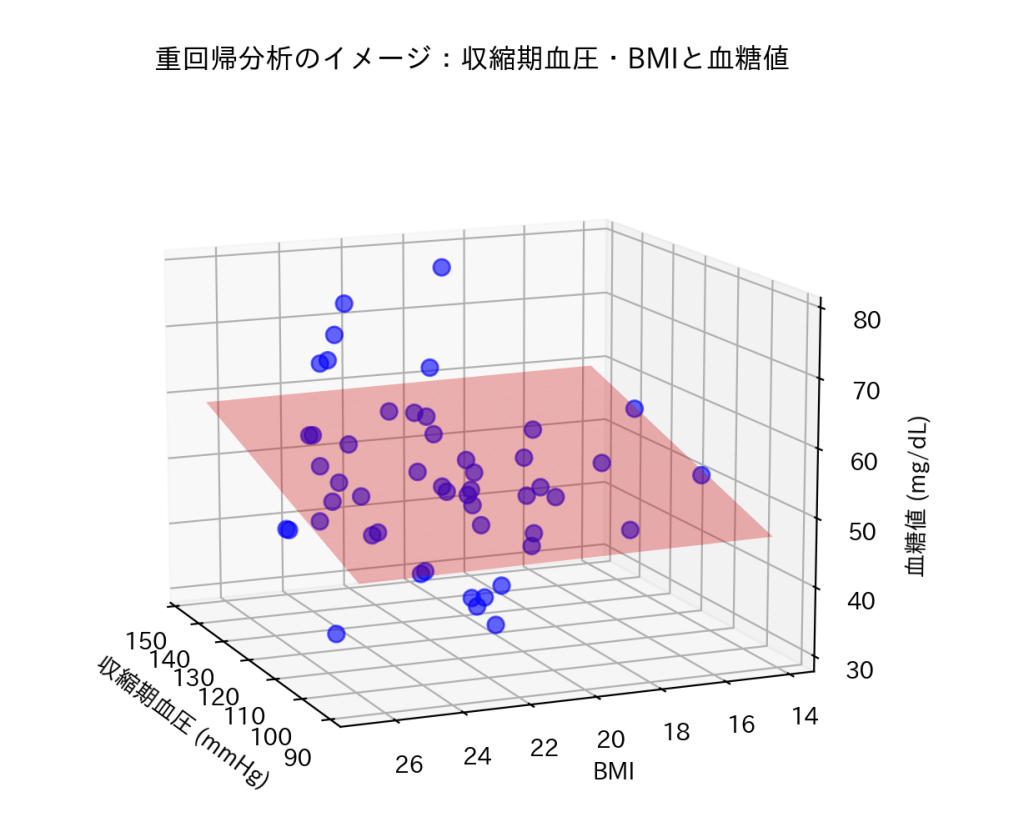
このように、3Dで結果を見ていくのです。
今回は収縮期血圧・BMIを説明変数、空腹時血糖を目的変数としています。

つまり、今回は収縮期血圧・BMIから空腹時血糖を予測する設定にしています
（もちろん、説明変数と目的変数を入れ替えることもできます）
赤の平面は、空腹時血糖と収縮期血圧・BMIの関係を示しています。

まず、同じ図でBMIと空腹時血糖の関係を見てみます。

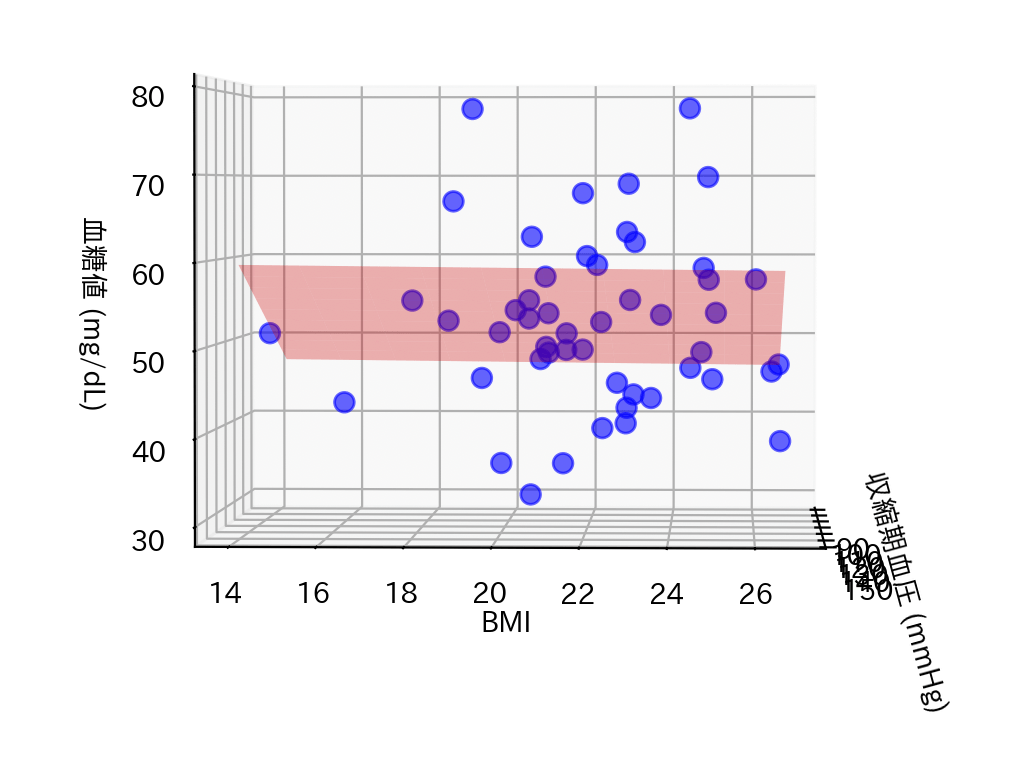
う〜ん、何だか赤い平面が広がっていますね。しっくり来ません。
今回の場合だとBMIと空腹時血糖はあまり関連があるとは言えないです。

続いて、収縮期血圧と空腹時血糖を比べてみましょう。

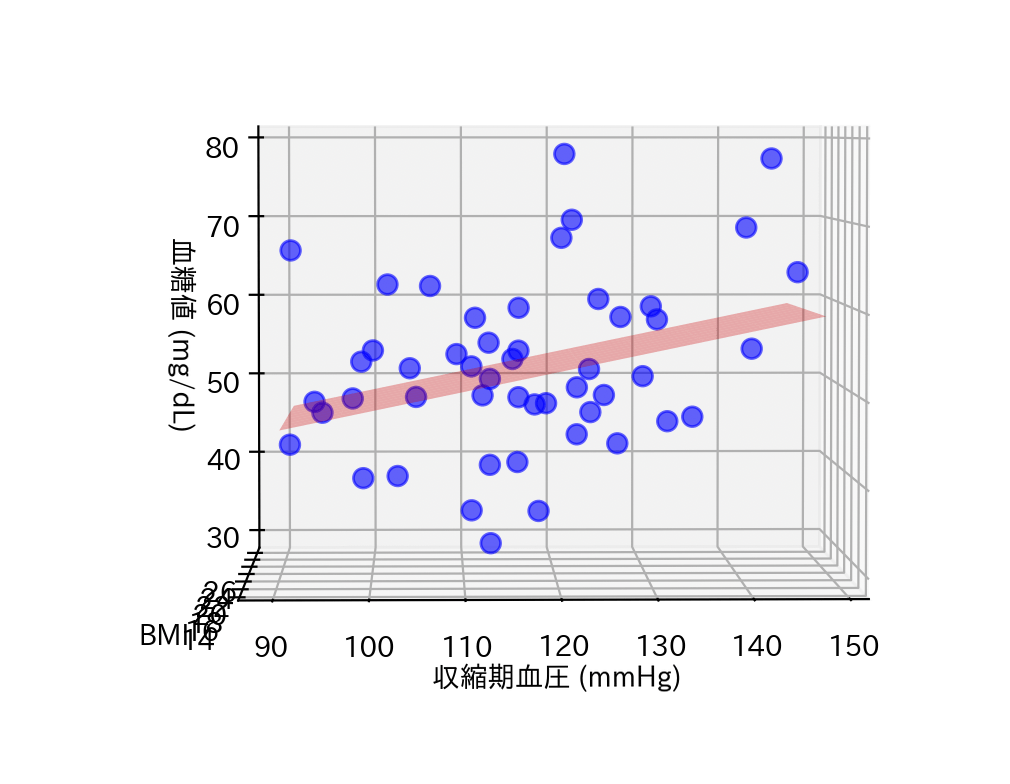
さっきより赤の平面が直線に近づきました。
これは収縮期血圧と血糖値は関連がある可能性があります。
ただし、あくまで可能性があるだけで、絶対に関連があるとは言えないのでご注意ください。

ロジスティック回帰

一方で、結果が「はい／いいえ」のような2択のとき（※場合によっては3択以上のこともあります）に使うのがロジスティック回帰です。

例：歩数とメタボ判定

• 説明変数：1日の歩数
• 結果：メタボあり＝1、なし＝0
  ※元々数字ではないものを数値化したものを「ダミー変数」と言います

分析すると、歩数が増えるほどメタボの確率が下がる、といったことがわかります。
そして「オッズ比」という便利な数字を使えば、
「1日8000歩以上歩く人は、そうでない人に比べてメタボ判定の確率が30％低い」といった形で示すこともできます。

グラフにすると、直線ではなく「S字カーブ」が出てくるのが特徴です。

直線で示そうとするとうまくいかないので、このようにS字カーブで表示されます。

まとめ

• 線形回帰 ： 結果を予測するためのもの。数値（血圧、BMI、空腹時血糖など）のデータを使う。
• ロジスティック回帰 ：結果を2択に分類するためのもの。数値と2択（病気あり／なし、治療効果あり／なしなど）のデータを使う。

どちらも、なんとなくのイメージを数字で裏付けられるのが魅力です。
「BMIが高いと血圧が高い気がする…」「歩数が多いと健康っぽい…」という感覚を、データで確かめられます。

さらに言えば、回帰分析は「統計学の基本」であると同時に、「機械学習の入り口」でもあります。
難しい機械学習の話にいきなり飛び込む前に、まずは回帰分析を押さえておくと安心です。

ぜひみなさんも、自分の身近な疑問を「回帰分析で調べたらどうなるかな？」と考えてみてくださいね。