中学生でも分かる！？機械学習の数学〜教師なし学習〜

恒例の「中学生でも分かる！？統計・機械学習の数学」の時間がやってきました。

まだ「教師なし学習」についてご存知でない方は、こちらの記事をご参照ください。

それでは、早速行きますよ！！レッツゴーーーー！！！

1. k平均法の数式

クラスタリングの王道である「k平均法」。
数式で書くとこうなります。

$\sum_{i=1}^{k} \sum_{x \in C_i} \lVert x - \mu_i \rVert^2$

登場人物：

① $\lVert x - \mu_i \rVert^2$

x：1つのデータ（例：A君の座標）
μ_i：クラスタiの中心（グループのリーダー的存在）
$\lVert x - \mu_i \rVert^2$ ：A君がグループリーダーからどれだけ離れているかの 距離の二乗

つまり、A君が近ければ近いほど（値が小さいほど）、グループに馴染みやすいということです。

② $\sum_{x \in C_i}$

∈：〜に属する、という意味です。a∈Aなら「aはAに属する」です。
この式自体は「クラスタiに属する全員について足し算する」という意味です。
「グループのメンバーみんなのリーダーからの距離を合計しよう」、といったノリです。

③ $\sum_{i=1}^{k}$

クラスタ（グループ）は一つではありません。全てのクラスタについて合計して考えます。
「グループ1、グループ2、…全部合わせて考えよう」というノリです。

つまりこの式は、

「各グループで、みんながリーダーからどれだけ離れているかを合計するよ！そしてそれを全グループでさらに合計するよ！」ということをします。

要するに「グループがバラバラじゃないように、できるだけ小さくしたい！」というゴールを表しているわけです。

2. 重心（平均）の更新式

では、先ほどの「グループリーダー」はどうやって決めているのでしょうか。

そう、その答えは平均です。

$\mu_i = \frac{1}{|C_i|} \sum_{x \in C_i} x$

登場人物：

$|C_i|$ ：クラスタiの人数
$\sum_{x \in C_i} x$ ：みんなの座標を足し算

つまり「みんなの位置を合計して人数で割れば、リーダー（重心）が決まる！」という考え方なのです。

図にすると、以下のようになります。

点の色はクラスタ（グループ）の違いを示しています。
それぞれのクラスタ中心（グループリーダー、×部分）が示されていますね。

3.階層クラスタリング

さて次は「階層クラスタリング」の式です。
こちらは「グループ間の距離」をどう測るか？で数式が変わります。

(1) 単連結法（single linkage）＝最短距離法

$D(A, B) = \min_{x \in A, \, y \in B} \lVert x - y \rVert$

登場人物：

A,B：2つのグループ
$\lVert x - y \rVert$ ：AのメンバーとBのメンバーの距離
min⁡：最小値をとる

つまり、「一番仲良しペアの距離がグループ間の距離！」という理屈です。

これも図にしてみました。

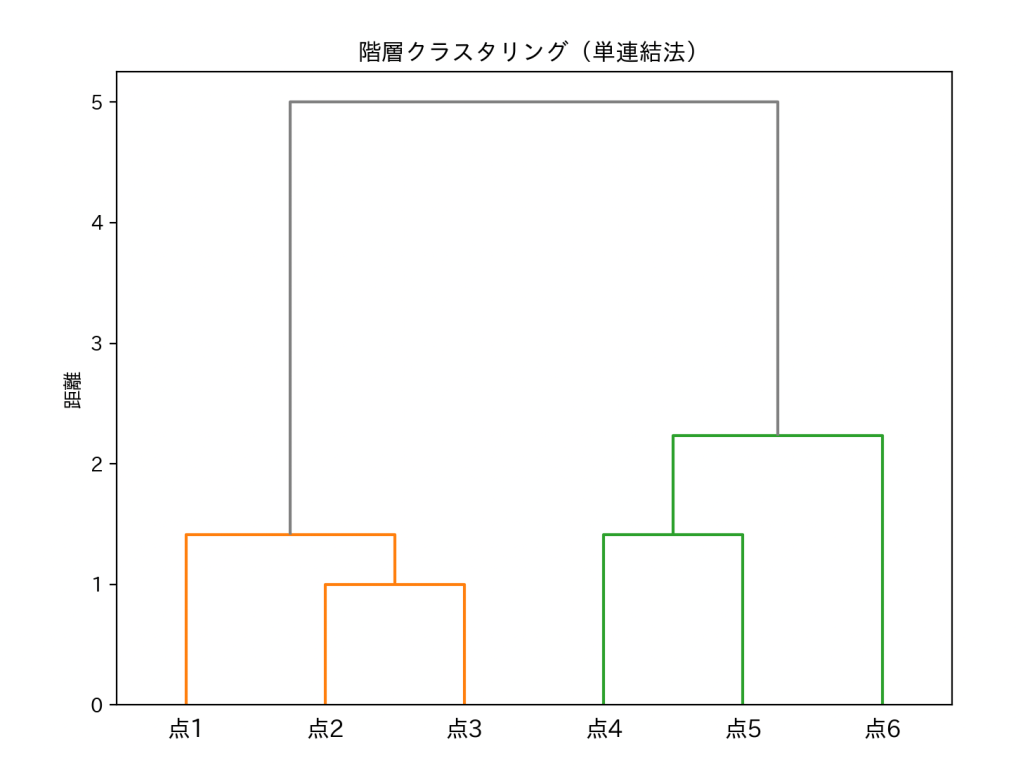
これは分類結果を木のように表した「デンドログラム」です。
横軸がデータ（点1〜点6）、縦軸が「距離」を表しており、枝がつながる位置がクラスタが結合した距離を意味しています。

したがって、図では「一部の点が近ければ全体が早く結合する」傾向が出ます。
距離が「5」の時点でオレンジと緑のクラスタがつながっています。

この考え方が単連結法です。

(2) 完全連結法（complete linkage）＝最長距離法

$D(A, B) = \max_{x \in A, \, y \in B} \lVert x - y \rVert$

さっきの式と似ていますが、こちらは、「min」ではなく「max」が使われています。

max：最大値をとる

「一番遠い人同士の距離がグループ間の距離！」という理屈です。
（つまり、全員がそこそこ仲良くないと同じグループにはならない厳し〜〜い方式です。世知辛い。）

では、こちらも図式化してみましょう。

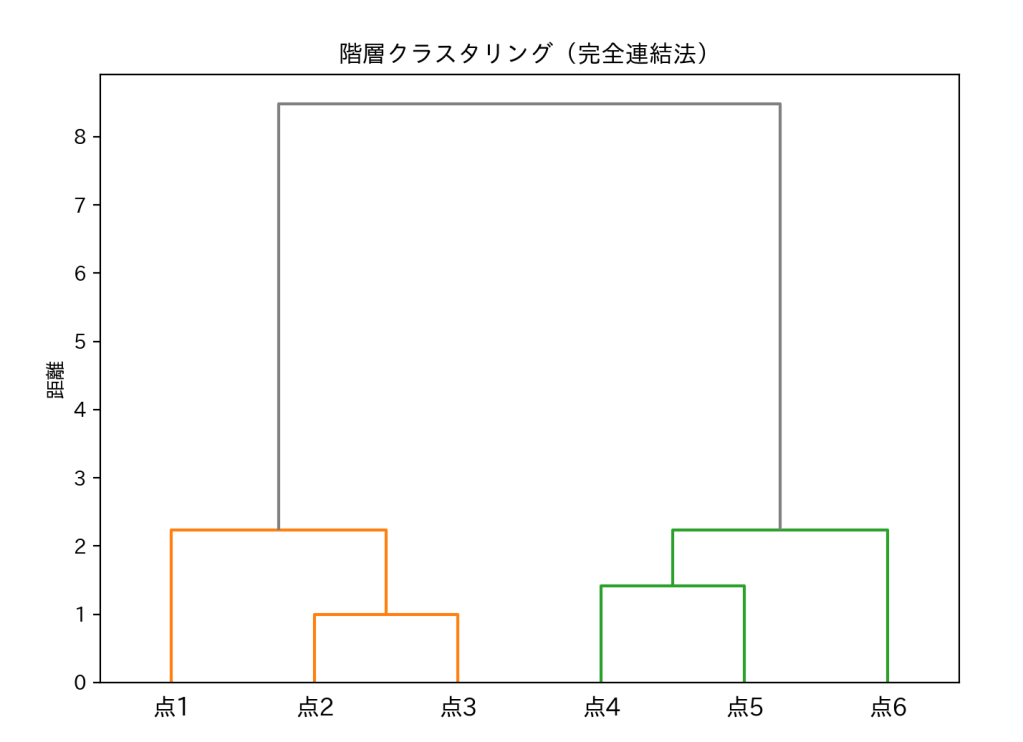
単連結法の時と比べてみてください。さっきより「距離」（グレーの部分）が長くなっていますね。
さっきは距離が「5」だったのが、今回は「8」と遠くなっています。

単連結法では「一番近い点同士」でグループをつなぐため、部分的に距離が近いだけでもすぐに結合してしまいます。
その結果、見かけ上「クラスタ同士が早めにくっつく」傾向が出ます。

一方、完全連結法では「一番遠い点どうしの距離」を基準にするため、
グループ内の全員がそれなりに近くならないと結合できません。
その分、クラスタが合体するのは遅くなり、図のように 縦軸（距離）の値が大きくなる のです。

(3)群平均法（average linkage）

$\displaystyle D(A,B)=\frac{1}{|A||B|}\sum_{x\in A}\sum_{y\in B}\,\lVert x - y\rVert$

登場人物：

${|A|,|B|}$ ：それぞれクラスタ A,Bの人数（データ点の数）
$\sum_{x\in A}\sum_{y\in B}$ ：Aの全ての点とBの全ての点をペアにして、距離を足し算
$\lVert x - y\rVert$ ：Aの点 x とBの点 y のユークリッド距離（＝2つの点のまっすぐな距離）
$\frac{1}{|A||B|}$ ：全てのペアの平均をとる

「クラスタAとクラスタBの距離＝両方のクラスタに属する全ペアの平均距離」です。
つまり、「平均的にどれくらい離れているか」でクラスタの近さを決める方法です。

これも図にしてみます。

右側の点の位置が変わっていますが、樹形図の描画上の都合であり、クラスタの結合関係は変わっていません。あまりお気になさらず。

群平均法は、単連結法のように一部の近い点に引っ張られることもなく、完全連結法のように一番遠い点だけで判断することもありません。
「クラスタ間の全体的な距離感」を基準にするため、バランスの良いクラスタが得られるのが特徴です。

(4)ウォード法（Ward法）

$\displaystyle D(A,B)=\frac{|A||B|}{|A|+|B|}\,\lVert \mu_A - \mu_B \rVert^2$

登場人物：

${|A|,|B|}$ それぞれのクラスタに含まれる点の数
$\mu_A, \mu_B$ :クラスタA, Bの重心（平均ベクトル）
$\lVert \mu_A - \mu_B \rVert^2$ ：クラスタAとBの重心の距離の二乗
$\frac{|A||B|}{|A|+|B|}$ ：AとBの大きさに応じた重みづけ（＝重要なデータや大きな集団の影響を大きく反映させる仕組み）

この式は「AとBを統合したときに、クラスタ内のばらつき（二乗誤差和）がどれだけ増えるか」を表しています。
つまり、 「クラスタをまとめても、ばらつきが一番小さくなる組み合わせ」を優先して結合する方法なのです。

これも同じく図にします。

クラスタAとBの大きさに応じた重みづけがされているため、小さなクラスタと大きなクラスタが合体するときも、不公平にならないよう調整されています。
実際の図を見ると、距離の縦軸が他の方法よりも高めになり、全体として「まとまりの良い」クラスタが形成されていることがわかります。

4. 行列計算で重心を求める

また、重心の計算は行列計算で求めることもできます。

例：データが3点あるとすると、

これを平均するには、

行列を「縦に合計して人数で割る」だけで、重心がすぐ出てきます。
難しく見えますが、実際の中身は「算数の平均」と一緒です。

行列についてもう少し詳しく知りたい方は、行列の記事をご参照ください。

単純に図にすると、以下のようになります。

複数の点の位置の平均を求めますよ、という意味です。

まとめ

今回の記事をまとめると、

k平均法(k-means)の式は「みんながリーダーから離れすぎないようにする」
重心は「ただの平均」
階層クラスタリングは「仲良し基準」をどう決めるか（最小 or 最大）
行列は、やってることは足し算と割り算

そう考えると、前よりは合点承知の助になれると思います。

それでは、また次の記事でお会いしましょう！！！

~~このブログ、統計の話がメインなのに、資格関係の話が一番読まれているの、正直複雑な気分でございますわ…~~

落ちこぼれナースの統計チャレンジ

中学生でも分かる！？機械学習の数学〜教師なし学習〜

1. k平均法の数式

2. 重心（平均）の更新式